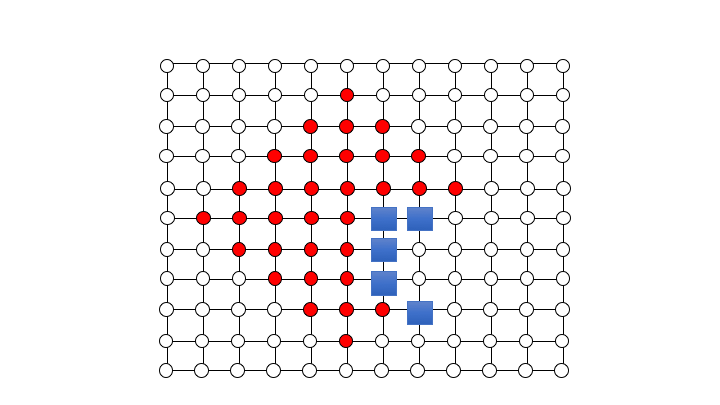
My research is the advancement of combinatorics knowledge with a focus on graph theory concepts, processes and designs. For the short-term, I strive to find a balance between working on new, innovative problems and classical, well-studied concepts. Many of the recent innovations are stated in the form of dynamic and discrete time graph processes.
Dynamic and discrete time processes can be used to model many fascinating games that have real-life applications. The "firefighter problem" models the percolation and containment of a fire over a map. The main goal is to determine the minimum resources needed to protect a certain proportion of the map. However, other important avenues of investigation include conditions under which the percolation of the fire is maximized and also minimizing the number of nodes a fire burns before being contained. These goals can be complicated by political needs that produce additional constraints. The problem can also be thought of as a virus spreading through a network, or information through a population. One can think of "eternal domination" as mobile resource allocation and movement of emergency response teams within a city. These mobile units must be situated and moved in such a way that they adequately respond to any sequence of events. It is often critical to maximize the use of resources. Of particular interest in discrete-time processes are complexity results, asymptotic behaviour and optimal design of networks.
About Us | Privacy Policy | Contact Us |The Department of Mathematics, Statistics and Computer Science, St. Francis Xavier University © 2018
