Figure 1 -Binocular Convergence and the "Trigonometry of the Eyes"

This animation shows how 18^th-century theorists thought that binocular convergence could give a precise, trigonometric calculation of the distance of an object.

The cross-section of the two eyes is based on an illustration from Descartes' Optics.

First the eyes fix an object a mile away -- let's imagine that it is the point of a church steeple.  The light rays from that point (in blue) are essentially parallel and that signals to the brain that the steeple is very far away.

Next, an arrow approaches and the eyes converge on its tip.  The nerves and muscles in the eyes sense the rotation in the eyesockets and somehow precisely measure two angles of rotation.

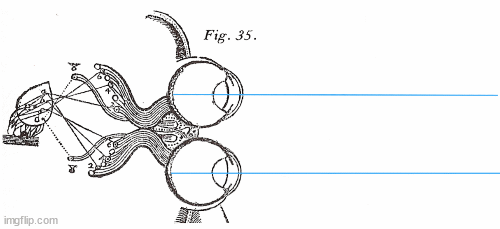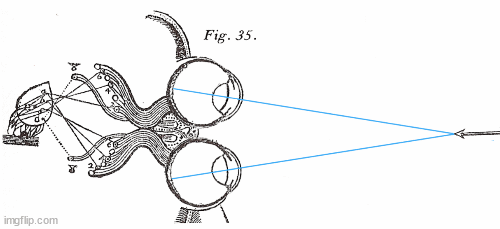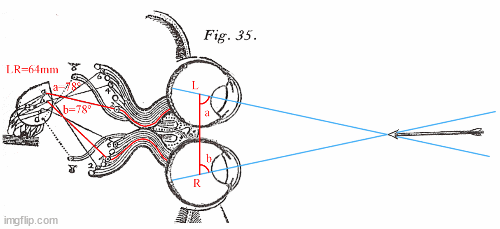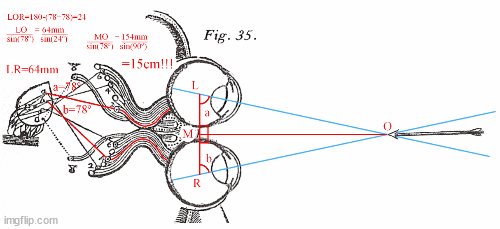
Here is where the theory becomes fanciful.  The brain instantly and unconsciously does complex trigonometric calculations (penciled in in red) to find the angle of convergence at point O and accurately calculate the distance OM.

I am not saying that binocular convergence is not important for depth perception.  It is.  Rather, it does not calculate absolute distances.  The stereoscope can be used to demonstrate that.