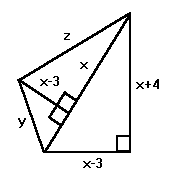Grade Eleven Problems
Grade Eleven Problems
1)
Betty and Tracy planned a 5000km trip in an automobile with
five tires, of which four are in use at any time. They plan to interchange
them so that each tire is used the same number of kilometers. What is the
number of kilometers each tire will be used?
Need A Hint?
Answer
2)
C is the center of the circle and F is a point on the circle such
that BCDF is a 2cm by 3cm rectangle. What is the area of the shaded region?
(in cm2).
Need A Hint?
Answer
3)
Allie has an income which is five eighths that of Basil. Allie's
expenses are one-half those of Basil and Allie saved 40% of his income.
What is the percentage of his income that Basil saves?
Need A Hint?
Answer
4)
Solve this problem:
If triangle DEF points A, B, and C are taken on DE,DF and EF respectively
such that EC = AC and CF = BC. If angle D = 40 degrees then what does angle
ACB equal (in degrees)?
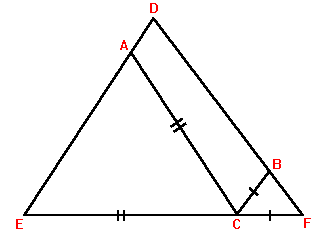
Need A Hint?
Answer
5)
A ladder leans against a vertical wall. The top of the ladder is
7m above the ground. When the bottom of the ladder is moved 1m farther
away from the wall, the top of the ladder rests against the foot of the
wall. What is the length of the ladder?
Need A Hint?
Answer
6)
7)
It takes 4 1/2 minutes for Elton John to listen to his favorite
song on a record recorded at 45 r.p.m. (revolutions per minute). One day,
Elton accidentally played this record at 33 1/3 r.p.m.'s. What was the
number of revolutions required to play the song? What was the amount of
time it took to play it at 33 1/3 r.p.m.?
Need A Hint?
Answer
8)
Todd and his brother have each agreed to mow half of the front lawn,
which is a 20m by 40m rectangle. The mower cuts a 1m wide strip. If Todd
starts at the corner and mows around the lawn toward the center, about
how many times around must he go before he has mowed his half?
Need A Hint?
Answer
9)
The Bunbury's want to build a deck on their cottage. The architect
drew them a diagram which shows it built on the corner of the cottage.
A railing is to be constructed around the four outer edges of the deck.
If AB = DE, BC = CD and the length of the railing is 30 metres, then what
dimensions will give maximum area?
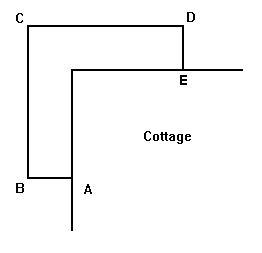
Need A Hint?
Answer
10)
11)
To mark her place in the book she is reading, Gillian always folds
the page as shown in the diagram so that the bottom-right corner touches
the opposite side of the same page. In the book, the pages are six inches
wide. What is the length in inches of the crease angle that Gillian makes
in terms of the angle O ?
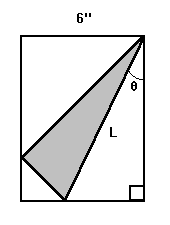
Need A Hint?
Answer
12)
A dog chasing a rabbit, which has a start of 45m, jumps 3m every
time the rabbit jumps 2m. In how many leaps does the dog overtake the rabbit?
Need A Hint?
Answer
13)
(a2 + b2) (c2 + d2) = (ac +\- bd)2 + (ad -\+ bc)2
Use it to write 481 as the sum of two squares in two different ways.
Need A Hint?
Answer
14)
How many times does the paper wind around the cardboard roller on
a 300 sheet roll of bathroom tissue? Each sheet is 12cm long. The diameter
of the full roll is approximately 9.6cm and the diameter of the cardboard
roller is approximately 4cm.
Need A Hint?
Answer
15)
Batman decided to go gambling one night. He has k dollars. He pays
$5.00 admission to enter a casino. While there he doubles his money. He
leaves and pays $5.00 for parking his Bat Mobile. He pays $5.00 to enter
a second casino. He again doubles his money, but when he pays $5.00 for
parking, he has no money left. Find k.
Need A Hint?
Answer
16)
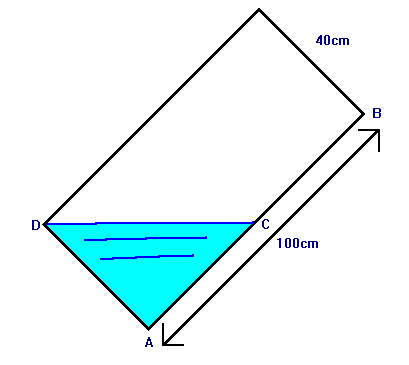
As shown in the diagram, a house is located at C on Lochaber
Island in a lake and another house is located at B. If the distance from
A to D is
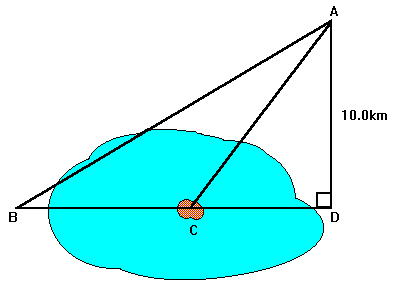 10.0km and angle <abc = angle <cab =28o . What
is the distance from B to C?
10.0km and angle <abc = angle <cab =28o . What
is the distance from B to C?
Need A Hint?
Answer
17)
At Upper Clements Park, a rollercoaster is constructed in such a
way that any car is y metres above the ground when it is x metres from
the starting point where y = 16 = 15 sin(Pi/60*x).
What is the height of the car in metres when x = 750? What is the
period of motion?
What is the maximum height the rollercoaster reaches?
What is the x value at this point?
Need A Hint?
Answer
18)
If the length of the hour and minute hand of a clock are 4cm and
6cm respectively, what is the distance in cm, between the tips of the hands
at two o'clock?
Need A Hint?
Answer
19)
20)
John and Mike were skipping off math class because they didn't do
their homework and they knew Mrs. Doyle would be checking. During their
time off from class, Mike decided to pull out his math book and do the
following problem....
It read:
For what values of r does the line y = 2x-3 intersect (at one or
more points) the circle x2 + y2 = r2.
He found one of the answers to be 1.
Was he right?
If not, what were all the answers?
Need A Hint?
Answer
21)
Arbor Drive has no numbers on houses, just names. Since the mailman
was having some trouble with the mail, it was decided to number them. One
side was numbered continously with odd numbers starting with 3. The first
building on the other side was a duplex, numbered 2 and 4, but somewhere
on that side there was a gap where houses had still to be built, and allowance
was made for eventual numbering.
When contacting their local Canadian Tire they found that each digit
cost 50 cents. The total bill for all the digits was $42.50 and the even-numbered
side cost $5.50 less than the other side.
When the gap is filled there will be exactly the same number of houses
on each side. What is the number of the last odd-numbered house, and what
are the missing numbers on the other side?
Need A Hint?
Answer
22)
It is an odd number with three digits. All the digits are different
and add up to 12. The difference between the first two digits equals the
difference between the last two digits.
What is the digit?
Need A Hint?
Answer
23)
Every graduating senior from Dr. John Hugh Gillis High enters St.
Francis Xavier University, as do one half of those from Guysborough High.
At St. F.X., one half of the freshman class are from Dr. John Hugh Gillis
High. If 400 graduates from Guysborough High and 300 from Dr. John Hugh
Gillis, how many of St.F.X. freshmen are neither from Dr. J. H. Gillis
nor Guysborough High?
Need A Hint?
Answer
24)
In a plane, four distinct lines intersect the interior of a circle
forming regions within the circle. If m represents the maximum number of
regions and n represents the minimum number, find m + n.
Need A Hint?
Answer
25)
You and your best friend Sparky are playing a game that involves
flipping a coin. Sparky has just flipped ten heads in a row. You, being
a bright person, are quite suspicious, but Sparky assures you that the
coin is a fair coin. If Sparky isn't lying, what is the probability that
the next toss of the coin will be heads?
Need A Hint?
Answer
26)
In Ottawa many fields have circular irrigation systems. A single
sprinkler is placed on the center of the field. If the sprinkler sprays
water just to the four edges of the field, what percent of the field is
not watered?
Need A Hint?
Answer
27)
Alf, Bert and Cash are suspects in a robbery case. Their trial reveals
the following facts: Either Cash is innocent or Bert is guilty. If Bert
is guilty then Cash is innocent. Alf and Cash never work together and Alf
never does a job on his own. Also, if Bert is guilty, so is Alf. Who is
guilty?
Need A Hint?
Answer
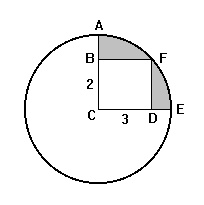
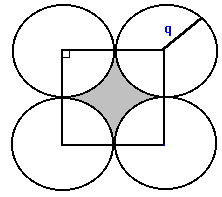
28)
If the area of each circle is the diagram is Pi/4 and the distance
between the centre of the circles P and Q is the square root of 3, what
is the area of ABCD not covered by the circles. (Hint: The circles are
congruent and are tangent to each other and to the sides of the rectangle).
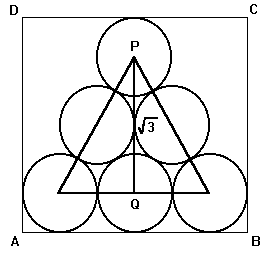
Need A Hint?
Answer
29)
30)
If 3 dice are thrown, in how many ways can we obtain a sum of 15?
(A toss of 6,6,3, is different from a toss of 6,3,6).
Need A Hint?
Answer
31)
The Chateau family has two cupboards for its wine bottles, a small
cupboard and one much larger. Being very fussy, they do not like their
wine exposed to the light more than 12 times, including both the time they
buy it and the time they drink it and each time they open the cupboard.
If they drink one bottle each day, how often does the Chateau family need
to buy wine?
Need A Hint?
Answer
32)
Jean Luc, a professional painter, decided to try something a little
different. He decided to create a mathematical work of art. He divides
a square piece of canvas into nine equal squares and paints the central
square red. He then divides each of the remaining eight squares into nine
equal squares, painting each of the eight central squares so formed yellow.
The remaining squares are again each divided into nine, the centers this
time being painted blue. This process is continued using a different color
for each new set of central squares until over half of the original area
of the canvas has been painted with paint. How many different colors have
been used and how many central squares have been painted?
Need A Hint?
Answer
33)
If a rectangular solid has sides, front and bottom faces with areas
of 2x, y/2 and xy cm2 respectively, what is the volume of the
solid in centimetres cubed?
Need A Hint?
Answer
34)
Line a1, has equation y = mx + b. Line a1 crosses the y axis at
p and line a2 crosses the x axis at q.
If pq is perpendicular to both lines, then what is the y intercept
of a2?
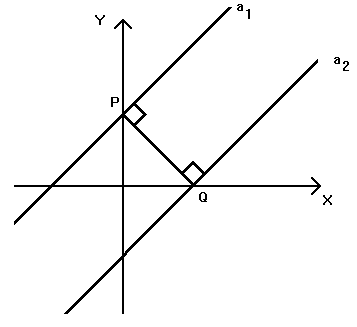
Need A Hint?
Answer
35)
a) What is the real value for x such that x log23 = log103
?
b) What is the value of (tan 45)*(cos 30 )* (sec 120)*(sin 150)*(cot
90)* (scs 315)?(all angles expressed in degrees)
Try this problem without a calculator.
Need A Hint?
Answer
36)
Five members of a basketball team are weighed and an average weight
is recalculated after each member is weighed. If the average increases
by one kilogram each time, how much heavier is the last player than the
first one? What if the difference is always two kilograms? Three kilograms?
Need A Hint?
Answer
37)
If Hypatia randomly takes a coin from her purse, its expected value
is 15 cents. If she had another dime, the expected value would be only
14 cents. What coins does she have in her purse ?
Need A Hint?
Answer
38)
Suppose that at the end of any year, a specific unit of money has
lost 10 percent of the value it had at the beginning of that year. What
is the smallest integer n such that after n years the unit of money will
have lost 90 percent of its value?
Need A Hint?
Answer
39)
A set of consecutive positive integers beginning with 1 is written
on the teacher's blackboard. A student came along and erased one number.
The average of the remaining numbers is 35 and 7/17. What number was erased?
Need A Hint?
Answer
40)
The integers greater than one are arranged in five columns as follows:
2 3 4 5
9 8 7 6
10 11 12 13
17 16 15 14
What column will contain the number 1000?
Need A Hint?
Answer
41)
Solve the following Geometry problem:
In a triangle ABC, M is the midpoint of the side BC, AN bisects angle
BAC, BN is perpendicular to AN. If sides AB and AC have lengths 14 and
19, then what is the length of MN?
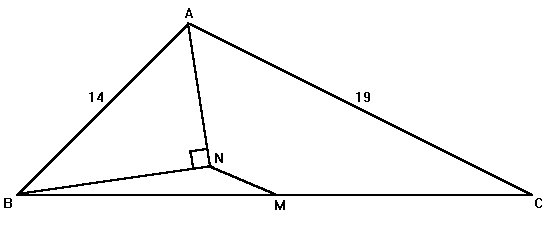
Need A Hint?
Answer
42)
Mark, Mike, Lawrence and Joshua bought a motorbike for $60.00. Mark
paid one half of the sum of the amounts paid by the other boys, Mike paid
one third of the sum of the amounts paid by the other boys; and Lawrence
paid one fourth of the sum of the amounts paid by the other boys. How much
did Joshua have to pay?
Need A Hint?
Answer
43)
Uncle Bert was making porridge in a cylindrical pan of diameter
24cm. The spoon he was using is 26 cm long. It accidentially falls and
sinks into the porridge. Calculate the minimum volume of porridge necessary
to hide the spoon. You may ignore the volume of the spoon.
Need A Hint?
Answer
44)
Fred and Jerome are out for a bike ride and Fred ran into a tree
dismantling his bicycle beyond repair. They were 16km from home. They decide
that Fred will start on foot and Jerome will start on his bike. After some
time, Jerome will leave his bike beside the road and continue on foot,
so that when Fred reaches the bike he can mount it and bike the rest of
the distance. Fred walks at 4 km per hour and rides at 10km per hour, while
Jerome walks at 5 km per hour and bikes at 12 km per hour. For what length
of time should Jerome ride the bike, if they are both to arrive at the
same time?
Need A Hint?
Answer
45)
Anyone can draw stars by using the following method. Start with
a circle and mark a number of points (n points) equally spaced around the
circumference. Now join each point to the one situated m points further
on, as shown.
Note: The third star consists of two like the first star, but the
second star cannot be split into smaller ones. How many different stars
of the unsplitable type can be drawn with n = 7, 8, 9, 10, and 15? Create
a table of your results.
Find the property which n and m must have for the corresponding star
to split up into two or more smaller stars.
Need A Hint?
Answer
46)
Three rectangles are lined up horizontally as shown. The first rectangle
has a width of 1 and a length of 2. The second rectangle has a width of
2 and a length of 4. The third rectangle has a width of 4 and a length
of 8. What is the area of the shaded region?
Need A Hint?
Answer
47)
Years ago, during a foreign war, a desert fort occupied by troops
lay under seige. The fort was square in shape with 8 defensive positions
- One at each corner and one in the middle of each side.
The fort commander General Gregorie LeVangie knew that the enemy
would not charge as long as they could see 15 active defenders on each
side, so with 40 troops under his command, he stationed 5 in each defensive
position. When one of his men was wounded he arranged the rest so that
the enemy could still see 15 on each side. How did he do this?
Further casualties occurred. Explain how, as each man falls, LeVangie
could rearrange his troops around the fort to prevent a concerted attack.
Reinforcement arrived just as the enemy was about to charge. How many active
defenders did they find left?
Need A Hint?
Answer
48)
A Chevette starts travelling east along a road. At the same time,
from the same point a Porche starts travelling north at a speed 15 km/hr
faster then that of car A. After one hour and twenty minutes, the cars
are 100km apart. At what speeds are they travelling?
Need A Hint?
Answer
49)
In a local pet store, the cats sold for $10.00 each and the canaries
sold for $15.00. The total value was $360.00. One night, the owner forgot
to close the door and the animals got loose. Two cats and half of the canaries
disappeared. If the total value was now $220.00, how many of each were
present before the escape?
Need A Hint?
Answer
50)
Legally married in Vancouver, my neighbor has reached an age that
is a square of some number. The product of the digits of his age is his
wife's age. The age of their daughter is the sum of the digits of the mother's
age. How old are they?
Need A Hint?
Answer
51)
The owner of a local jewellery store hired 3 watchmen to guard his
diamonds, but a thief still got in and stole some diamonds. On the way
out, the thief met each watchman, one at a time. To each he gave 1/2 of
the diamonds he had then, and 2 more besides. He escaped with one diamond.
How many did he steal originally?
Need A Hint?
Answer