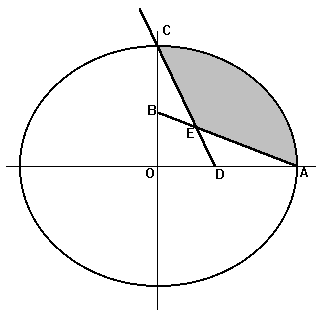Grade Twelve Problems
 Grade Twelve Problems
Grade Twelve Problems
1)
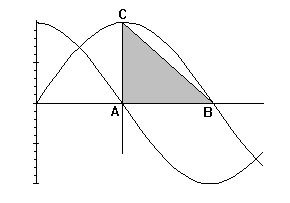
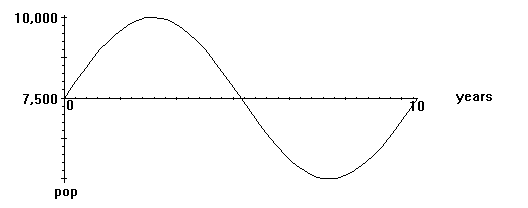
The population of a certain species in the wild varies according to a
sine curve over a period of 10 years. Using the diagram, determine at
what time the population will be at a minimum in the 10 year period.
Need A Hint?
Answer
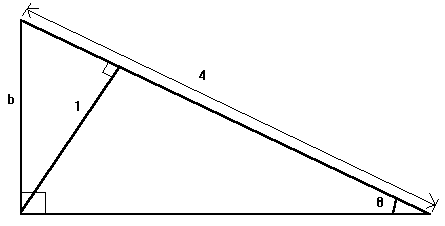
2)
A right triangle in the first quadrant is bounded by lines y = 0, y = x,
and y = -x+5. Find its area.
Need A Hint?
Answer
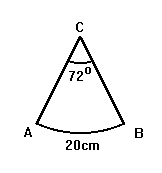
3)
A cone is formed with an arc length AB equal to 20 cm. As the cone is
formed from a sector of a circle with angle 72 degrees, determine
a) the radius of the circle from which the sector is taken, and
b) the radius of the base of the cone formed by sector ABC
Need A Hint?
Answer
4)
Given three rectangles of area A, with the following dimensions, find
the values of x and y and determine the area of each quadrilateral.
(i) (ii) (iii)
length x x-3 x+3
width y y+2 y-1
Need A Hint?
Answer
5)
f(x) = 5 sin x
g(x) = 5 cos x
If the period of both curves is 2Pi, find the area of triangle ABC, given
point C is at the maxima of f(x) and points A and B both touch g(x), and
f(x) respectively where g(x) = f(x) = 0.
Need A Hint?
Answer
6)
A farmer has 160m of fence to enclose a four sided field. He is going to
use all or part of one side of his barn so he can make his field as big
as possible. If his barn is 100 m long, find the maximum area of his field.
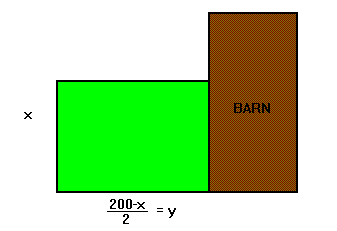
Need A Hint?
Answer
7)
A parabola with vertex (2,0) and axis of symmetry parallel to the y-axis,
passes through (3,1) and (-3,t). Find the value of t.
Need A Hint?
Answer
8)
Find the area of triangle ABC where
- angle ABC = 35 degrees
- angle BCA = 110 degrees
- angle CAB = 35 degrees
AND, length BC = 4 cm
Need A Hint?
Answer
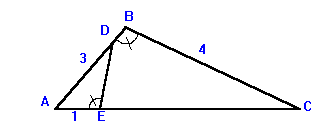
9)
Angle ABC = Angle DEA
length AB = 3
BC = 4
AE = 1
Find length of ED.
Need A Hint?
Answer
10)
A swimming poool is 30 m wide, 50 m long and 7 m deep. After an
earthquake, the pool is tilted along one edge (AB) and the water
completely covers side ABCD. At this point, 3/4 of the base is
covered by water. What was the water level before the earthquake?
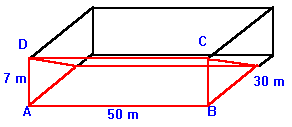
Need A Hint?
Answer
11)
A van travels a maximum of 100 km/h. Its speed decreases in proportion
with the number of passengers. The van can carry a maximum of seven
people. Given that the van can travel 88 km/h with 3 people in the van,
what will be the speed of the van when 6 people are on board?
Need A Hint?
Answer
12)
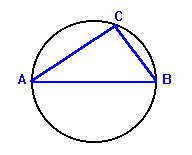
In this diagram, AB is the diameter of the circle. If AB is 10 cm and
the area of the triangle is 11 cm2, find the perimeter of triangle ABC.
Need A Hint?
Answer
13)
Nine large pipes will drain a pond in eight hours and six small pipes
will drain the same pond in sixteen hours. How long will it take 3 large
pipes and 5 small small pipes to drain the pond?
Need A Hint?
Answer
14)
Two cars race around a circular track, in opposite directions, at
constant rates. They start at the same point and meet every 30 seconds.
If they move in the same direction, they meet every 120 seconds. If the
track is 1800 m long, what is the speed of each car?
Need A Hint?
Answer
15)
If point C is any point on circle A and circle B is drawn such that its
circumference bisects the circumference of A. If the area of circle A is
pi find the area of shaded part.
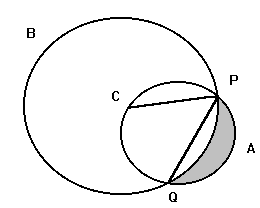 Need A Hint?
Need A Hint?
Answer
16)
Given the graph of line y = x intersects a parabola at point
A = ([1- (17)1/2 / 2] , [1-(17)1/2 / 2])
and B = ([1+(17)1/2 / 2] , [1-(17)1/2) / 2]) and the parabola has y
intercept (0,-4), find the equation of the parabola.
b = 0 4 = a(-1 + 17)/4
Need A Hint?
Answer
17)
Find the value(s) of d such that 5x2 + 5(d - 3)x - 9d2 + 15d + 30 = 0
has one real root.
Need A Hint?
Answer
18)
The remainder when f(x) = 4x4 + 10x3 + kx2 + bx - 2 is
divided by x + 1 is -3, when f(x) is divided by x-1 the remainder is 25.
Determine the remainder when divided by x + 2.
Need A Hint?
Answer
19)
Find m and k so that the quartic function m2x4 + 5x3 + k2x2 + 5mkx + 6mk
has remainder 32 when divided by x + 1
and remainder 72 when divided by x.
Need A Hint?
Answer
20)
A chemical company spends x million dollars on research and finds that
its profit can be expressed as a function of the amount of money spent on
research. If Profit(x)= 30 + 6 log (x+2) how much will the company have to
spend on research to increase its profit from its present level, with a
research investment of 5 million dollars (P(5)), to 80 million dollars.
Need A Hint?
Answer
21)
PR and QR are tangent to a circle
with center O that has radius 1.
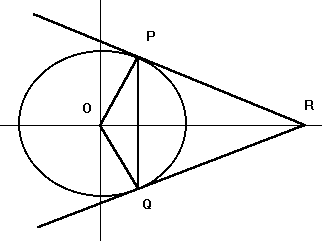
P = (1/2, 31/2/2)
Q = (1/2, -31/2)
using what you know find the length of OR and determine angle
Need A Hint?
Answer
22)
Find and solve a system of equations given the following information.
Three people go to a store where there is a sale. Every shirt in the
store are x dollars, all pants are y dollars and all sweaters are
z dollars. One person buys two shirts, one pair of pants and one
sweater, The second person buys one shirt, two pairs of pants and two
sweaters. The third person buys three shirts and four pairs of pants.
Find the price of each item if the first person spent $155 and the second
and third person spent $235 each.
Need A Hint?
Answer
23)
A carís headlights make two circular bright spots on a wall when the car
is 10 m away. At what rate is the area of the bright spots changing when
the car is 6 m away. The velocity of the car is 3 m/s. see diagram
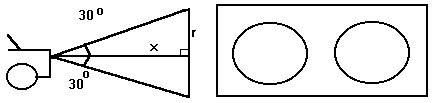
Need A Hint?
Answer
24)
Find the maximum area of a quadrilateral with sides parallel to the
coordinate axes that can be inscribed in the finite region bounded by
y1 = (1/4) x2 and y2 = 2 - (1/4) x2
Need A Hint?
Answer
25)
The curves of equation y1 = (1/4) x2 y2 = 2-(1/4)x2
intersect at (-2, 1) and another point A. Find the angle between the
curves at A (the angle between two curves corresponds to the angle
between their tangents).
Need A Hint?
Answer
26)
A biologist finds that when a culture of bacteria is left for x days the
number of live bacteria will be P(t) = 2000 + 6000 lg(t + a). The
original number of bacteria is 2572 (rounded from 2572.55). How
many bacteria will there be after seven days?
Need A Hint?
Answer
27)
A motor boat leaves a ship and travels due north at 80 km/h. The ship
proceeds 30 degrees south of east at 32 km/h. If the motorboat has
enough fuel for 4 hours what is the maximum distance north that it
can travel so that it can safely return to the ship.
Need A Hint?
Answer
28)
Find ax2 + 3x - 5 = y such that it intersects y = - 1/2x - 6 at
two points in the third quadrant and crosses the x axis at -3 +/- (19)1/2.
Need A Hint?
Answer
29)
For what values of x will y1 >= y2
y1 = - (1/3)x2 + 4x - 2
y2 = (1/4)x2 - 1
Need A Hint?
Answer
30)
Three circles with centers A, B and C are tangent to each other. Each
circle has radius 5. Lines DE and FG are tangent to C and intersect at
G. Find the length of FG.
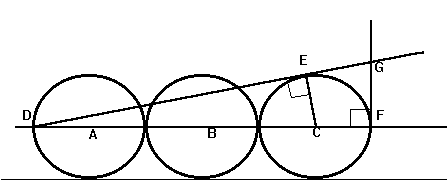
Need A Hint?
Answer
31)
32)
The polynomial x4 + bx3 + 59x2 + cx + 60 is exactly divisible
by x2 + 4x + 3. Find the values of b and c.
Need A Hint?
Answer
33)
The equations y = mx - 3 and y = 5/(2x + 3) intersect at x = 1 and x =
a. Find the values of m and a.
Need A Hint?
Answer
34)
A car traveling at 40 m/s (144 km/h) passes a police car hidden behind a
billboard. Two seconds after the car passes the billboard the police
car is on the road accelerating at 3.0 m/s squared. How long will it
take the police to catch the speeder.
Need A Hint?
Answer
35)
36)
Radium decays exponentially with time, it has a half life of 25 years.
If a chemist leaves 0.500 kg of Racium on a shelf how much will be left
in 5 years time? If there were 0.700 kg left after 10 years what would
the initial amount have been?
Need A Hint?
Answer
37)
An unknown chemical is found to lose 15 % of its original mass over a
period of 20 years. What is its half life?
Need A Hint?
Answer
38)
The position of a swinging pendulum is traced by the curve below. The
angular frequency of the pendulum is w = (g/l)1/2 where g is 10.0 m/s
squared and l is the length of the pendulum.
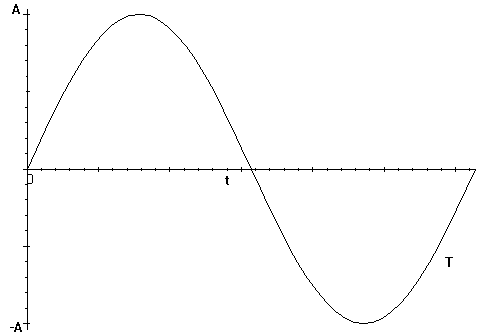
If the pendulum is of length 40 m, then find the period and the equation
of motion. (note T = 1/p = 2 pi/w).
What is the position of the pendulum at t = 5s?
Need A Hint?
Answer
39)
The level of water in a funnel drops at a rate of 2m/min. At what rate
is the surface area of the water changing when the water is 3m high?
Need A Hint?
Answer
40)
If the lines whose equations are:
y - x - 2 = 0
y - 3x + 2 = 0
3y - kx - 4 = 0
All pass through the same point, find the value of k.
Need A Hint?
Answer
41)
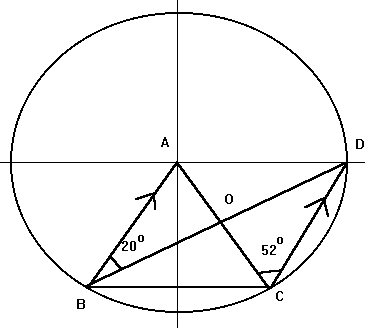
In this diagram the center of the circle is A, angle ABD equals 20
š and angle DCA equals 52š. Find angle BOC.
Need A Hint?
Answer
42)
43)
44)
In this diagram the equation of the circle is x2 + y2 =
16. D = (2, 0), B = (0, 2), C = (0, 4),
A = (0, 4). Find the shaded area.
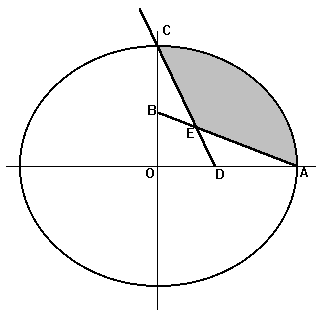
Need A Hint?
Answer