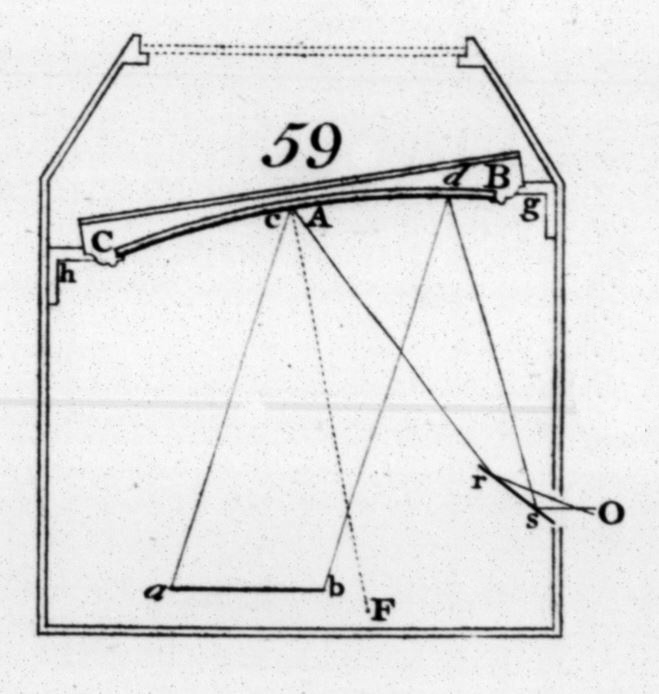
Figure 1 – Harris' Mirror Box

Optical boxes, which enhance the 3D illusion of engraved images, are usually fitted with a biconvex lens, but there are many descriptions of ones using concave mirrors instead. Some say they created a better 3D illusion than the lensed boxes. None have survived so I have long been intrigued by them and wanted to build one.

Figure 2 – Laser Eyes

Joseph Harris (1775) offers a couple of designs for such a box, one of which is illustrated in figure 1. In this cross-section, CB is the concave mirror and ab is the image-plate that holds the engraving. The observer, at O looks at the concave mirror through the angled mirror rs.

Before I to build one on this or another design, I want to understand the principles first. My method is first to set up a configuration of a mirror and an image that works to produce the desired effect (Figure 2). In figure 2 you can see an original 18th-century vue d'optique which was a kind of wide-angle engraving that the lens or mirror is supposed to enhance.

I found that the best 3D view was with my eyes at the top of the image plate looking over it towards the mirror – where the two laser-sights are now positioned (figure 2).

The laser setup mimics looking at a point at the back of the depicted cathedral. You can see in figure 2 the red laser origins as dots in the laser-sights and the point of convergence as the red dot on the print where the back of the nave of the cathedral is meant to be.

Harris thinks that the ideal distance between the mirror and the image is a little less than the focal length of the mirror (figure 1). This mirror (figure 2) has a 30 cm focal length and I find that the distance between mirror and print at which the depth illusion is greatest is 21 cm. This is a surprise and a cause for some head-scratching.

Figure 3 – Laser Measure

What is even more surprising is that the eyes diverge at that setting. You can see that in figure 3 where I have turned down the mirror to see where the two lasers would intersect without it. I was expecting an intersection, but you can see that the dots on the whiteboard are further apart than the laser origin points. The distance apart is wider the further away you position the whiteboard.

With a little trigonometry I measure the divergence and find that each eye turns outward 1.17º from parallel. Nearly parallel is what they would be if they were looking to the back of the nave of a real cathedral. Parallel is what they would be looking to infinity. Divergent would suggest that we are seeing beyond infinity which is, first of all, incoherent and secondly, not at all what the image looks like at this setting. There is something wrong with the strictly mathematical understanding of binocular convergence that Harris and his contemporaries were working with to explain this 3D illusion.