1. Algorithm Analysis

An algorithm is a clearly specified set of simple instructions to solve a problem.

There are different ways to solve the same problem, so different algorithms.

Consider that two students propose their own algorithm to find the optimal path in a maze.

• How can we compare these algorithms?

• Which one is better?

  • In terms of computation time?

  • In terms of memory consumption?

  • How does it scale?

1.1. Mathematical Background

To estimate the time or the memory consumption, we need some tools, mathematical tools.

Given two functions, there are usually points where one function is smaller than the other.

So it doesn’t make sense to claim that \(f(x) < g(x)\).

What we really want is to compare their relative rates of growth.

Before continuing, we need to define some things first.

Definition 1

\(T(N) = O(f(N))\) if there are positive constant \(c\) and \(n_0\) such that \(T(N)\leq cf(N)\) when \(N \geq n_0\).

This is what we call the Big-Oh notation.

Example

• Consider an algorithm that needs \(T(N) = n^2 + 5n + 25\) operations.

• We want to show that the algorithm Is \(O(n^2)\).

• So we want to show that:

  • there are constants \(n_0\) and \(c\)

  • such that for all \(n>n_0\), \(cn^2 > n^2 + 5n + 25\).

One way we can do this is finding a point where:

\[cn^2 = n^2 + 5n + 25\]

Consider \(n_0 = n\) then we calculate:

\[c = 1 + \frac{5}{n_0} + \frac{25}{n_0^2}\]

We can easily evaluate it for \(n_0 = 5\), and it gives us \(c=3\).

S0 \(3n^2 > n^2 + 5n + 25\), for \(n>5\)

Usually we do not apply this definition formally.

When we say that \(T(N) = O(f(N))\), we are guaranteeing that the function \(T(N)\) grows at a rate not faster than \(f(N)\).

Meaning than \(f(N)\) is an upper bound on \(T(N)\).

Example

\(N^3\) grows faster than \(N^2\), so we can say \(N^2 = O(N^3)\).

To make it easier we have a set of rules.

Rule 1

If \(T_1(N)=O(f(N))\) and \(T_2(N) = O(g(N))\), then

1. \(T_1(N) + T_2(N) = O(f(N)+g(N))\), intuitively it is \(O(\max(f(N),g(N)))\)

2. \(T_1(N)\times T_2(N) = O(f(N)\times g(N))\)

Rule 2

If \(T(N)\) is a polynomial of degree \(k\), then \(T(N) = O(N^k)\).

Rule 3

\(log^k N = O(N)\) for any constant \(k\).

It tells us that logarithms grow very slowly.

It is sufficient to arrange most of the common functions by the growth rate:

Function	Name
c	Constant
\(log N\)	Logarithmic
\(log^2 N\)	Log-squared
\(N\)	Linear
\(N^2\)	Quadratic
\(N^3\)	Cubic
\(2^N\)	Exponential

Important

As you can see what we want is to know is the growth rate is compared to the size of the input \(N\).

If we were comparing algorithms to sort elements in a list.

Depending of the time complexity and the number of elements, the running time to sort the list can be very different:

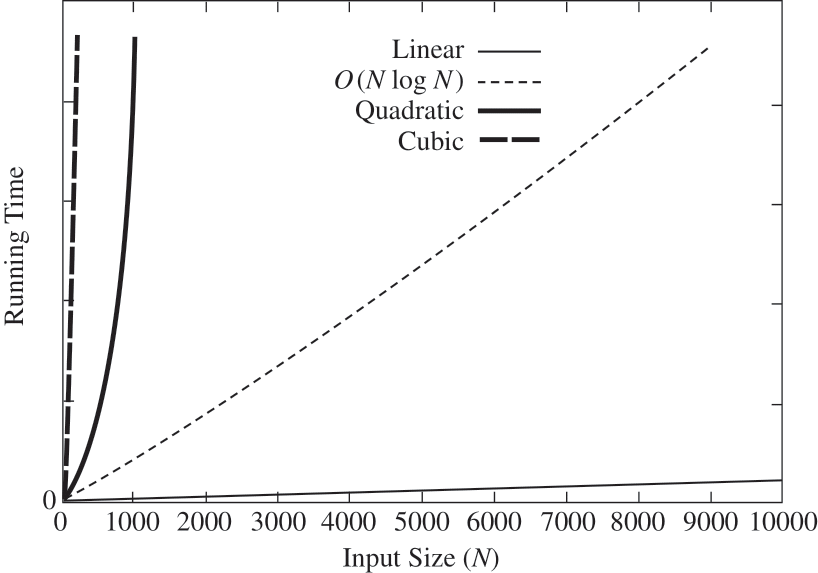
Or to give another idea:

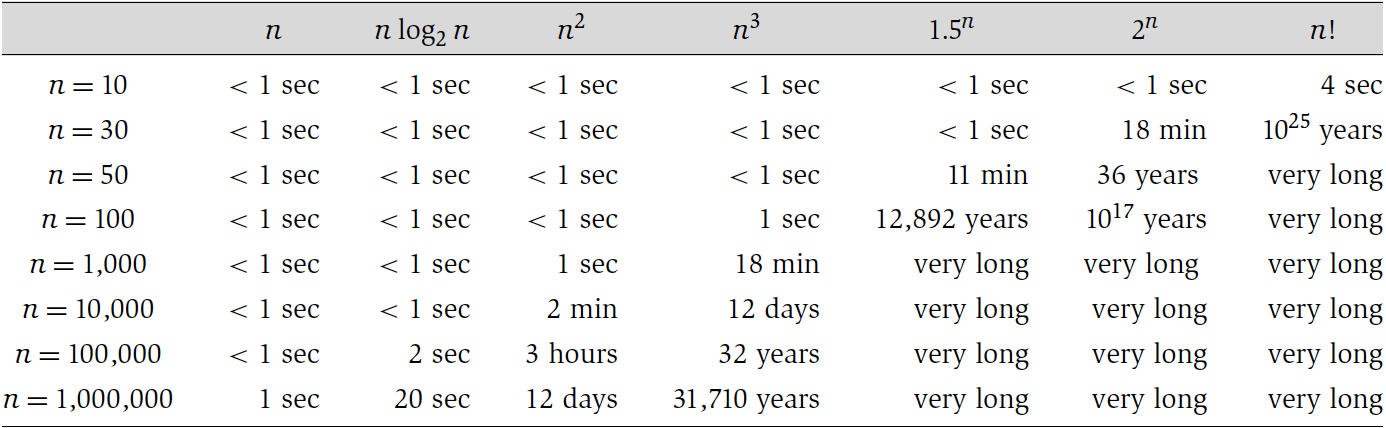
1.2. Running-Time Calculation

There are several ways to estimate the running time of a program.

The previous table was obtained empirically, meaning runs the algorithms and compare the results.

To simplify the analysis we will always consider that there is no particular unit of time.

We just want to calculate for an algorithm the Big-Oh running time.

• We throw away the low-order terms.

• We never underestimate the running time of the program. It should never finish after this upper bound.

1.2.1. Simple Example

Here is a simple program function to calculate \(\sum_{i=1}^N i^3\).

int sum(int n){
    int partialSum;

    partialSum = 0;
    for (int i = 1; i <= n; i++){
        partialSum += i*i*i;
    }
    return partialSum;
}

Activity

• How many units of time does it cost to declare a variable? (line 2)

• How many units of time for line 4 and 8?

• How many units of time for line 6 when executed once? How many times is it executed?

• How many for line 5?

• The total? And the corresponding Big-Oh?

1.2.2. General Rules

We will four rules to estimate the running time of an algorithm.

Rule 1 – For loops

The running time of a for loop is at most of the running time of the statement inside the for loop (including tests) times the number of iterations.

Rule 2 – Nested loops

The total running time of the statement inside a group of nested loops is the running time of the statement multiplied by the product of the sizes of all the loops.

Example

The following code has a running time of \(O(n^2)\).

k = 0;
for (int i = 0; i < n; i++){
    for (int j = 0; j < n; j++){
        k++;
    }
}

Rule 3 – Consecutive Statements

The running time of consecutive statements is just the sum of the running time of each statement.

Example

The following code is \(O(n^2)\).

for (int i = 0; i < n; i++){
    a[i] = 0;
}
for (int i = 0; i < n; i++){
    for (int j = 0; j < n; j++){
        a[i] += a[j] + i + j;
    }
}

It has a first for loop that run in \(O(n)\).

The second run in \(O(n^2)\).

Rule 4 – If/Else

The if/else statement is not as simple as it seems.

Usually these statements have the following structure:

if ( condition ){
    statement_1
}
else{
    statement_2
}

The running time cannot be more than the running time of the statement plus the larger running time between statement_1 and statement_2.

Important

Calculating it this way can overestimate the running time, but not underestimate it.

What happen if there is a recursion?

It depends on the type of recursion.

Some are just a for loop, such as the following function:

long factorial(int n){
    if(n <= 1){
        return 1;
    }
    else{
        return n * factorial(n-1);
    }
}

In this case, we can calculate the running time of the for loop (In this case \(O(n)\)).

Other recursion cannot be transformed into a simple loop.

long fib(int n){
    if (n <= 1){
        return 1;
    }
    else{
        return fib(n-1) + fib(n-2);
    }
}

The analysis is simple.

• Let \(T(N)\) be the running time for fib(n).

• If \(N=0\) or \(N=1\)

  • Then the running time is some constant value

  • \(T(0) = T(1) = 1\).

• For \(N > 2\)

  • The time to execute the function is the constant work of line 2.

  • Plus the work on line 6.

    • It consists of the addition of two function calls.

    • fib(n-1), so \(T(N-1)\)

    • fib(n-2), so \(T(N-2)\)

  • it gives us a total running time of \(T(N) = T(N-1) + T(N-2) + 2\)

We can prove that for \(N > 4, fib(N) \geq \frac{3}{2}^N\).

This recursion function is growing exponentially with the size of the input.

Activity

Discuss and gives some idea why this function is growing exponentially.

1.3. Maximum Subsequence Sum Problem

We will take a very practical problem. One that is very very common in technical interview.

Maximum Subsequence Sum Problem

Given an array of integers os size \(N\). Find the continuous subarray that maximize the value \(\sum_{k=i}^j A_k\).

Example

For the array [-2, 11, -4, 13, -5, -2], the answer is 20 (from a[1] to a[3]).

1.3.1. A first algorithm

It is very easy to come with a first algorithm:

Algorithm 1

    /**
     * Finds maximum sum in subarray.
     * @param a Vector of elements
     * @return Maximum contiguous sequence sum.
     */
    public static int maxSubSum(Vector<Integer> a){
        int maxSum = 0;

        for( int i = 0; i < a.size( ); ++i ){
            for( int j = i; j < a.size( ); ++j ){
                int thisSum = 0;

                for( int k = i; k <= j; ++k ){
                    thisSum += a.get(k);
                }

                if( thisSum > maxSum ){
                    maxSum   = thisSum;
                }
            }
        }
        return maxSum;
    }

Activity

1. Convince yourself that this algorithm works.

2. Analyze the running time.

3. Can we do better?

1.3.2. A second algorithm

It is possible to avoid the cubic running time by removing a for loop.

Of course most of the time it’s not possible, but in this case there is an inefficiency.

Notice that in the previous algorithm (line 13) is calculating \(\sum_{k=i}^j a_k\).

Which is the equivalent of \(a_j + \sum_{k=i}^{j-1} a_k\) making algorithm 1 inefficiency.

We then can deduce a more efficient algorithm:

Algorithm 2

    /**
     * Finds maximum sum in subarray.
     * @param a Vector of elements.
     * @return Maximum contiguous sequence sum.
     */
    public static int maxSubSum2(Vector<Integer> a){
        int maxSum = 0;

        for( int i = 0; i < a.size( ); ++i )
        {
            int thisSum = 0;
            for( int j = i; j < a.size( ); ++j )
            {
                thisSum += a.get(j);

                if( thisSum > maxSum ){
                    maxSum = thisSum;
                }
            }
        }
        return maxSum;
    }

Activity

1. Convince yourself that this algorithm works.

2. Analyze the running time.

3. Can we do better?

1.3.3. Divide-and-Conquer

For this problem, we can use a divide-and-conquer strategy.

The idea:

• The divide part:

  • We split the problem on two suproblems.

  • We solve each subproblem recursively.

• The conquer part:

  • Joining the two solutions.

  • Doing additional work.

In this problem, the maximum subsequence sum can be in one of three places.

• It occurs entirely in the left part.

• It occurs entirely in the right part.

• It occurs in both parts.

Consider the example:

First half	Second half
4 -3 5 -2	-1 2 6 -2

• The maximum subsequence sum for the first half is 6 (from \(a_0\) to \(a_2\)).

• The maximum subsequence sum for the second half is 8 (from \(a_5\) to \(a_6\)).

• The maximum subsequence in the first half that includes the last element is 4 (from \(a_0\) to \(a_3\)).

• The maximum subsequence in the second half that includes the first element is 7 (from \(a_4\) to \(a_6\)).

• Thus, the maximum subsequence that spans both halves and goes through the middle is \(4+7 = 11\) (from \(a_0\) to \(a_6\)).

Activity

1. Convince yourself that this algorithm works.

2. Create the function int maxSumRec( Vector<Integer> a, int left, int right )

• The first is step is to define the base case. If there is one element left == right.

• Calculate the center

• Calculate the max subsequence on the left side and right side.

• Calculate the max subsequence that spans both halves.

• Return the maximum between the three subsequences.

3. Analyze the running time.

We can analyze the algorithm.

• Let \(T(N)\) be the time it takes to solve a maximum subsequence sum problem of size \(N\).

• If \(N=1\) (the base case), the program take some constant amount of time.

• Otherwise the function performs two recursive calls.

  • It is done on a subproblems of size \(N\).

  • It takes \(T(N/2)\), for a total of \(2T(N/2)\).

• Combining the two subsequences require two successive for loops.

  • The work inside them is constant.

  • The amount of work is \(O(N)\)

• The total time is \(2T(N/2) + O(N)\).

• it gives us the following equation:

\[\begin{split}\begin{cases} T(N) = 1, &\mbox{if } N=1 \\ T(N) = 2T(N/2) + O(N), &\mbox{otherwise } \end{cases}\end{split}\]

We need to express \(T(N)\) in Big-Oh notation. We will see later how to do that precisely, but for now we just want a rough estimation.

For now \(T(N) = 2T(N/2)+N\).

• \(T(1) = 1\)

• \(T(2) = 4 = 2*2\)

• \(T(4) = 12 = 4*3\)

• \(T(8) = 32 = 8*4\)

The pattern is obvious, if \(N = 2^k\), then \(T(N) = N * (k+1) = N \log N+N = O(N \log N)\).

We improved from \(O(n^3)\) to \(O(N\log N)\)!

1.3.4. Achieving \(O(N)\)!

OK, now assume that we can achieve linear time complexity to calculate the maximum subsequence.

What does it imply?

• Maximum one for loop.

• Constant work in the loop.

Important

Almost all linear algorithms have these limitations!

Activity

Can you find the logic behind this algorithm?

This algorithm is a lot easier than the recursive algorithm and have better performance.

Warning

In the examples, we never try to memorize what is the maximum subsequence. We only returned the value of the maximum subsequence.

That’s how we maintain a low complexity.

The logic:

• If a[i] is negative, then it cannot be the start of the maximum subsequence.

• Any negative subsequence cannot prefix the maximum subsequence.

  • If the subsequence between a[i] to a[j] is negative we can advance i.

  • We can advance it to j+1.

    • Consider p any index between i+1 and j.

    • Any subsequence starting a p is not larger than the previous subsequence from a[i] to a[p-1].

    • j being the first index that causes the subsequence to in negative.

    • Thus advancing i to j+1 is safe

Important

The correctness is not obvious and would need to be proven.

The corresponding function is simple:

Algorithm 4

    /**
     * Linear-time maximum contiguous subsequence sum algorithm.
     *
     * @param a Vector of elements.
     * @return Maximum contiguous sequence sum
     */
    public static int maxSubSum4( Vector<Integer> a )
    {
        int maxSum = 0, thisSum = 0;

        for( int j = 0; j < a.size( ); ++j )
        {
            thisSum += a.get(j);

            if( thisSum > maxSum )
                maxSum = thisSum;
            else if( thisSum < 0 )
                thisSum = 0;
        }

        return maxSum;
    }

Activity

Convince yourself that this algorithm works.

1.4. Logarithms in the Running Time

Below a linear running time, there is logarithm running time.

The logarithm time usually appear around the general rule:

An algorithm is \(O(\log N)\) if it takes constant time (\(O(1)\)) to cut the problem size by a fraction (often \(\frac{1}{2}\)).

Important

if constant time is required to reduce the problem by a constant amount (such as to make the problem smaller by 1), then the algorithm will be \(O(N)\).

Only a special kind of problem can be \(O(\log N)\).

If you have a problem with an input of size \(N\), then you will need O(N) just to read the input.

So \(O(\log N)\) algorithms presume that the input is preread/preprocessed.

I will just give one example: the binary search algorithm.

Binary search

Given an integer \(X\) and a sorted array \(a\) find \(i\) such as \(a_i = X\).

You should already know this algorithm so I will not spend a lot of time on it.

The implementation is simple:

Binary Search

    /**
     * Apply binary search on a sorted list of elements.
     * @param a Vector of sorted elements.
     * @param x Element to find in the array.
     * @return The element if found or -1.
     */
    public static int binarySearch(Vector<Integer> a, int x){
        int low = 0, high = a.size() -1;
        while(low <= high){
            int mid = (low + high) / 2;

            if (a.get(mid) < x){
                low = mid + 1;
            }
            else if (a.get(mid) > x){
                high = mid -1;
            }
            else{
                return mid;
            }
        }
        return -1;
    }

Activity

1. Convince yourself that the algorithm works.

2. Analyze the running time.

1.5. Limitations of Worst-Case Analysis

Sometimes the analysis is shown to be an overestimate.

When it’s the case, the analysis needs to be tightened.

It may be that the average running time is significantly less than the worst-case running time and no improvement in the bound is possible.

For many complicated algorithms, the worst-case happens very rarely.

Calculating the average case is very complex (in many cases unsolved), and a worst-case bound is the best analytical result known.