4. Binomial Queues

4.1. Introduction

  • Consider a problem in which you use a priority queue.

  • Now, you receive another priority queue.

  • You need to merge both of them.

Activity

  • How do you proceed?

  • It seems difficult to design a data structure that efficiently supports merging.

  • Meaning that the operation is in \(O(N)\).

  • Merging require copying one array into another.

  • So, \(O(N)\).

  • How can we solve this for priority queues.

4.2. What is a Binomial Queue?

The Binomial Queues ADT needs to have the following operations:

  • Insertion

  • Deletion

  • Merging

Every operation are \(O(\log N)\) in the worst-case.

However, insertion takes constant time in average.

4.3. Structure

The most interesting thing about a binomial queue is its structure.

It’s not a heap-ordered tree, like binary heaps, but a collection of heap-ordered trees.

Note

A collection of trees is called a forest.

The idea:

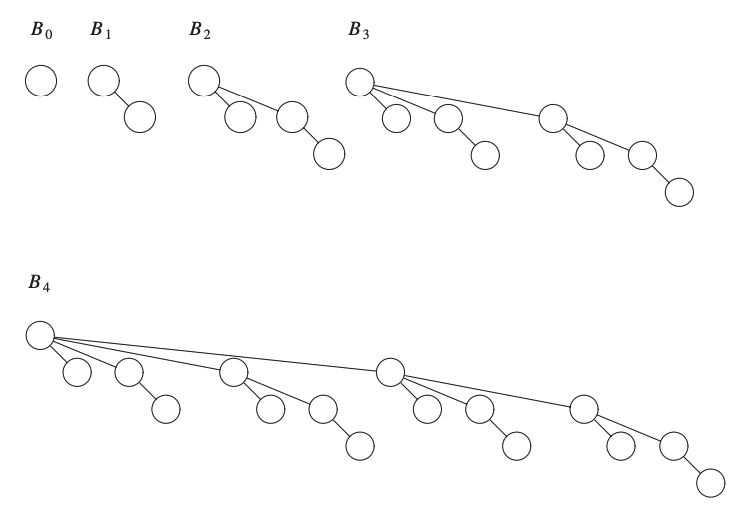
  • Each heap-ordered tree in the binomial queues is a binomial tree.

  • There is at most one binomial tree of every height.

  • \(B_k\) is a binomial tree of height \(k\).

  • \(B_k\) is formed by attaching \(B_{k-1}\) to the root of another \(B_{k-1}\).

Example

  • A binomial tree of height 0 is a one-node tree.

  • Etc…

The following figure illustrates different binomial trees.

../../_images/binomial_trees.png

Important

  • Binomial trees of height \(k\) have exactly \(2^k\) nodes.

  • The number of nodes at depth \(d\) is the binomial coefficient \(\binom{k}{d}\).

4.4. Binomial Queue Operations

We need to discuss the three main operations of the binomial queues.

4.4.1. Merging

  • Merging is an easy operation.

  • We will use an example.

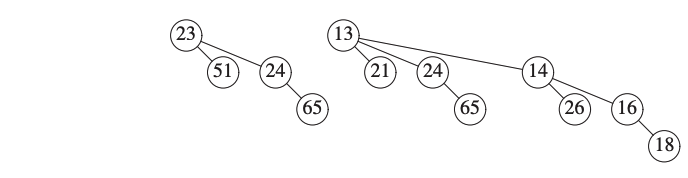
We consider the following binomial queues.

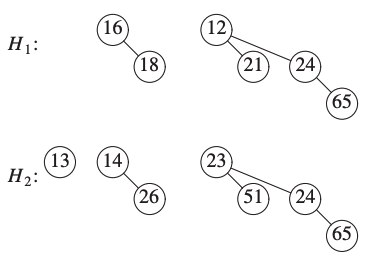
../../_images/merge_01.png

  • We define \(H_3\) the new binomial queue.

  • We need to take care of the \(B_0\).

  • \(H_1\) does not have a binomial tree of height 0.

  • \(H_2\) does, so we can just add it to \(H_3\).

../../_images/merge_02.png

  • Now we consider the binomial tree of height 1.

  • \(H_1\) and \(H_2\) have binomial trees of height 1.

  • We merge them by making the larger root a subtree of the smaller tree.

  • We obtain a binomial tree of height 2.

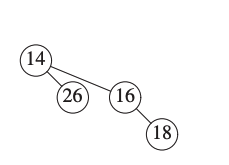
../../_images/merge_03.png

  • There are now three binomial trees of height 2.

  • We keep one binomial tree of height 2 and merge the other two.

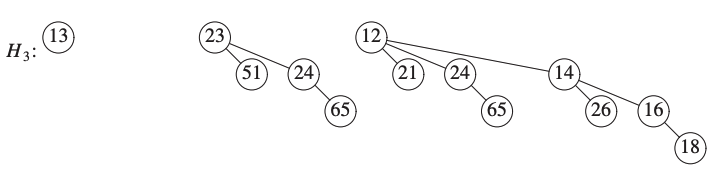
../../_images/merge_04.png

  • Since \(H_1\) and \(H_2\) have no trees of height 3 we stop there.

4.4.2. Insert

  • Insertion is a special case of merging.

  • We create a one-node tree (tree of height 0) and perform a merge.

The worst-case time of this operation is \(O(\log N)\).

Example

  • In this example we will insert the integers from 1 to 7 to an empty binomial queue.

  • We start by inserting 1.

../../_images/insert_01_binomial.png

  • We now insert 2.

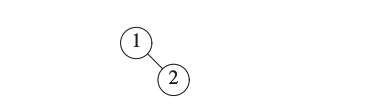
../../_images/insert_02_binomial.png

  • We now insert 3.

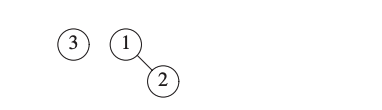
../../_images/insert_03.png

  • We now insert 4.

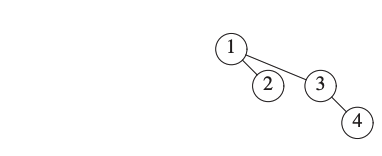
../../_images/insert_04.png

  • We now insert 5.

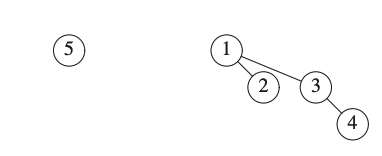
../../_images/insert_05.png

  • We now insert 6.

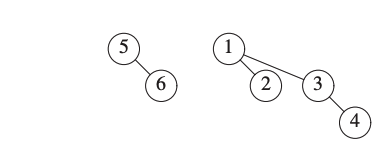
../../_images/insert_06.png

  • We now insert 7.

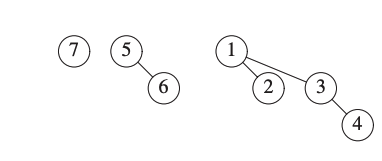
../../_images/insert_07.png

4.4.3. DeleteMin

  • Consider a binomial queue denoted \(H\).

  • Delete the minimum element by finding the smallest root.

  • Let this tree be \(B_k\).

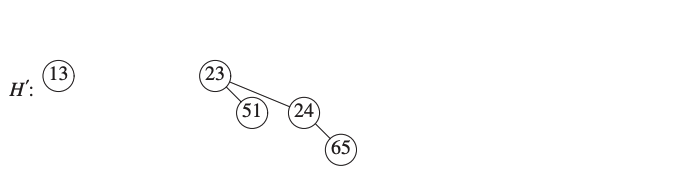
  • Remove it from \(H\), creating a new queue \(H'\).

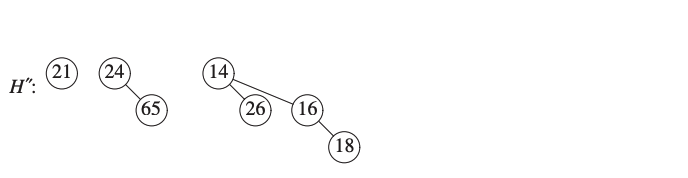
  • Remove the root of \(B_k\).

  • It creates binomial trees \(B_0, B_1, \dots, B_{k-1}\) in a queue \(H''\).

  • Merge \(H'\) and \(H''\).

Example

  • Consider the following binomial queue \(H\).

  • We want to remove the smallest element(\(12\)).

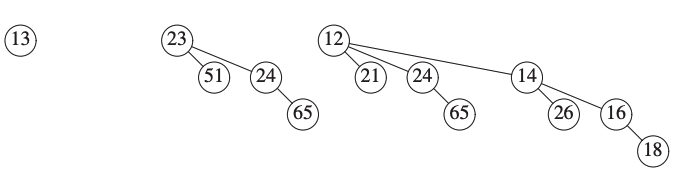
../../_images/delete_01_binomial.png

\(H\)


  • We remove \(B_3\) from \(H\) creating \(H'\).

../../_images/delete_02_binomial.png

  • We obtain \(H''\) the binomial queue creating after deleting 12 from \(B_3\).

../../_images/delete_03_binomial.png

  • We are merging \(H'\) and \(H''\).

../../_images/delete_04_binomial.png