Topic 12 - Graph
Graphs are a special type of data structure.
They are used to solve many problems, such as the shortest path problem.
However, if the implementation is not done carefully it can be too slow to use.
What is a graph?
We will start by giving a definition of a graph.
Definition: Graph
A graph \(G = (V,E)\) consists of a set of vertices \(V\) and a set of edges \(E\).
Each edge is a pair \((v, w)\), where \(v,w\in V\).
Edges are sometimes referred as arcs and vertices as nodes.
Directed Graphs
Definition: Directed Graph
When the edges (or arcs) \((v,w)\) are ordered the graph is directed.
Vertex \(w\) is adjacent to \(v\) if and only if \((v,w)\in E\).
Directed graphs are also referred as digraphs.
The following figure represents a digraph:
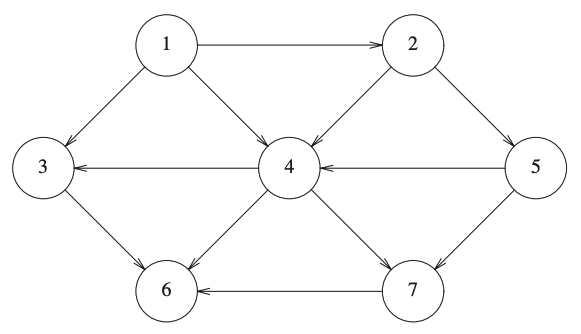
Activity
Write all the pairs \((v,w) \in E\) of the previous graph.
Undirected Graphs
If there are directed graphs, there are undirected graphs!
Definition: Undirected Graph
In an undirected graph with edges \((v,w)\in E\), there is an edge \((w,v)\in E\).
\(w\) is adjacent to \(v\) and \(v\) is adjacent to \(w\).
Activity
Take the previous graph and transform it to an undirected graph.
Draw the undirected graph that contains the following edges:
\(E = \{(a,b), (b,a), (a,c), (c,a), (b,c), (c,b)\}\)
Representing graph in memory
Obviously, we cannot represent a graph like this in memory.
We could be as close as possible to the math representation:
Storing a list of nodes
And storing the list of arcs.
Activity
What do you think about this representation?
Do you have a better representation?
There are two ways to represent a graph in memory:
Adjacency matrix
Adjacency list
Adjacency Matrix
The easiest way to represent is with a 2D matrix.
This is called an adjacency matrix.
The idea:
Consider a matrix \(M\).
For each \((u,v) \in E\):
We set \(M[u][v]\) to 1.
Otherwise to 0.
Example
If we take the previous graph.
We can create the following adjacency matrix.
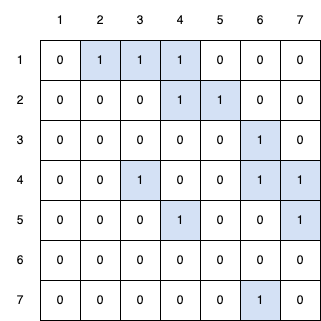
It is very easy to use adjacency matrix and very fast.
However, the space requirement is \(O(|V|^2)\).
It is a lot if the graph has a lotof nodes, but few arcs.
It is appropriate, if the graph is dense \(|E| = O(|V|^2)\).
Activity
Why using a matrix for dense graphs is not a problem?
In most problems, graphs are not dense.
Example
Consider a street map of a city.
Assume a Manhattan-like orientation.
Any intersection is attached to roughly 4 streets.
So, if the graph is directed with two-way streets.
The number of edges is \(|E| \approx 4|V|\)
If there are 3 000 intersection.
The number of vertices is 3 000.
And the number of edges is 12 000.
It requires an array of size 9 000 000.
A graph that is not dense is called sparse.
We need another way to represent sparse graph.
Adjacency List
Adjacency list are a better solution when the graph is sparse.
For each vertex, we keep a list of all adjacent vertices.
Example
If we take the previous graph.
We can create the following adjacency list.
The space requirement is \(O(|E|+|V|)\).
It is linear in the size of the graph.
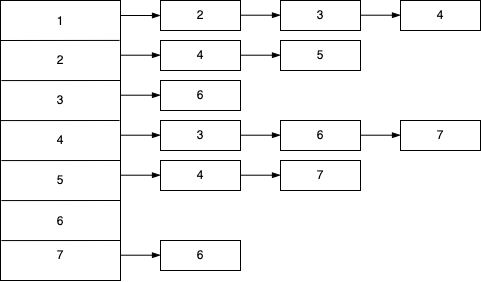
Activity
Why are we not using adjacency lists for dense graphs?
Weighted edges
Consider a problem in which you need to represent the streets and intersections in a city.
You would like to store the distance of each street.
A graph allows us to add weights on edges.
The changes to the previous representation are small:
Adjacency matrix: Instead of 0 and 1, we have the weight of the edge if it exists. If not \(- \infty\) or \(+ \infty\).
Adjacency list: Add a new element in the list.
Activity
Draw the directed graph that contains the following edges:
\(E = \{(a,b,2), (b,a,4), (a,c,3), (c,a,1), (b,c,10)\}\)
Give the adjacency matrix and adjacency lists representation.
More Definitions
Graphs are used in a lot of algorithms.
To use them in these algorithms, we require some last definitions.
Definition: Path
In a graph, a path is a sequence of vertices \(v_1, v_2 \dots, v_N\) such that \((v_i, v_{i+1})\in E\) for \(1 \leq i < N\).
The length of the path is the number of edges on the path (\(N-1\)).
Definition: Cycle
In a cycle in a directed graph is a path of length at least 1 such that \(v_1 = v_N\).
In undirected graph the edges need to be distinct.
If a directed graph does not have a cycle, it is called a acyclic graph.
Activity
Consider the graph given in the first example.
Give an example of a path.
Give a example of a cycle.