Topic 9 - \(O(1)\) Hash Tables
In some application, we want to guarantee a \(O(1)\) worst-case cost.
Suppose that all \(N\) items are known in advance.
If a separate chaining implementation could guarantee that each list had at most a constant number of items we would be done.
We know that as we make more lists, the lists will be shorter on average.
If we have enough lists, then we could expect no collisions at all.
This approach creates two problems:
The number of lists might be large.
We could still have collisions.
Perfect Hashing
Perfect hashing was theorized to solve the second problem.
Suppose that we have \(TableSize = M\), with \(M\) sufficiently large to guarantee that the probability fo collision is at least \(\frac{1}{2}\).
When there is a collision, we clear out the table and try with another hash function.
If there is another collision, we repeat the process with a third hash function.
Etc…
The expected number of trials will be at most 2 (since the probability of success is \(\frac{1}{2}\)).
How large \(M\) needs to be?
Remember that \(M\) is the number of list/cells in the hash table.
We should have a table of size \(M=N^2\) to guarantee a probability of \(\frac{1}{2}\).
Theorem
If \(N\) balls are placed into \(M=N^2\) bins, the probability that no bin has more than one ball is less than \(\frac{1}{2}\).
Proof
We call it a collision when two balls \(i\) and \(j\) are placed in the same bin.
Let \(C_{i,j}\) the expected number of collisions produced by any two balls \(i\) and \(j\).
The probability of any two specified balls to collide is \(\frac{1}{M}\).
Thus \(C_{i,j} = \frac{1}{M}\).
The expected number of collisions in the entire table is \(\sum_{(i,j), i<j}C_{i,j}\).
Since there are \(N(N-1)/2\) pairs it sums to \(N(N-1)/(2M) = N(N-1)/(2N^2)< \frac{1}{2}\).
The only issue is using \(N^2\) is impractical.
How to solve this issue?
Instead of using a linked list in case of collisions, we can use hash tables.
The idea:
Is to create a table of size \(N\).
Each time there is a collision for a cell, creates a hash table quadratic in size.
To illustrate the idea we have the following figure:
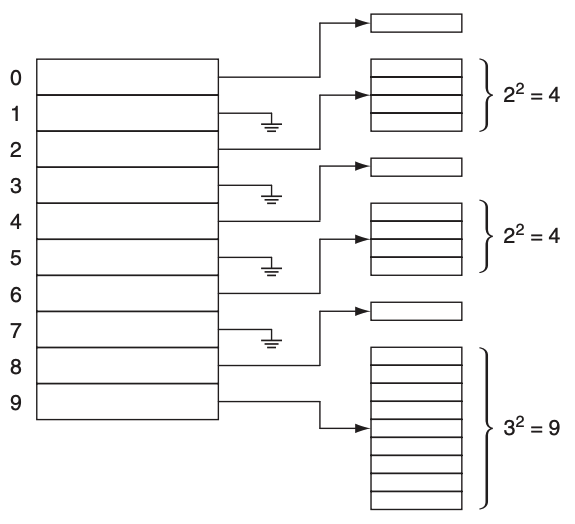
Each secondary hash table will use a different hashing function.
This strategy is called perfect hashing. We need to show that the size of the secondary hash tables is expected to be linear.
Theorem
If \(N\) items are placed into a primary hash table containing \(N\) bins, then the total size of the secondary hash tables has expected value at most \(2N\).
Proof
We use the same logic as in the previous proof.
The expected number of collisions is \(N(N-1)/2N = (N-1)/2\).
Let \(b_i\) the number of items hashing in the cell \(i\).
The size of the secondary table is \(b_i^2\).
The number of collisions for the secondary table is \(b_i(b_i - 1)/2\) called \(c_i\).
Thus the amount of space \(b_i^2\) is \(2c_i+b_i\).
The total space is then \(2\sum c_i + \sum b_i\).
The total number of collisions is \((N-1)/2\).
So we obtain a total secondary space requirement of \(2(N-1)/2 +N < 2N\).
It’s all good, but it only works if we know in advance the number of elements.
Cuckoo Hashing
Cuckoo hashing is a table scheme using two hash tables \(T_1\) and \(T_2\) each with \(N\) bins with independent hash functions.
The idea:
An item can be stored only one table.
The insertion try to insert the element in the first table.
If it is occupied, it evicts the existing item.
Then it tries to insert the evicted item in the alternative table.
If it is occupied, it repeats the process.
Example
The idea can be illustrated by a small example.
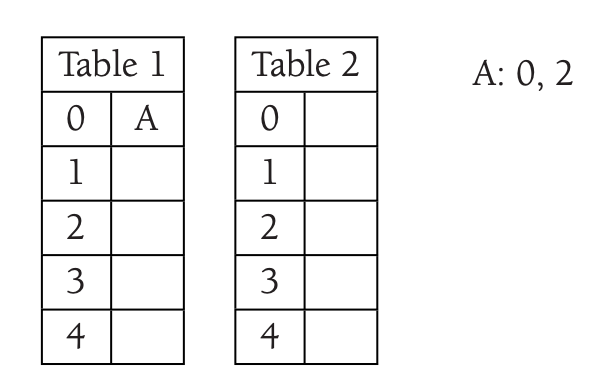
We are inserting A. A can take either the index 0 in \(T_1\) or 2 in \(T_2\).
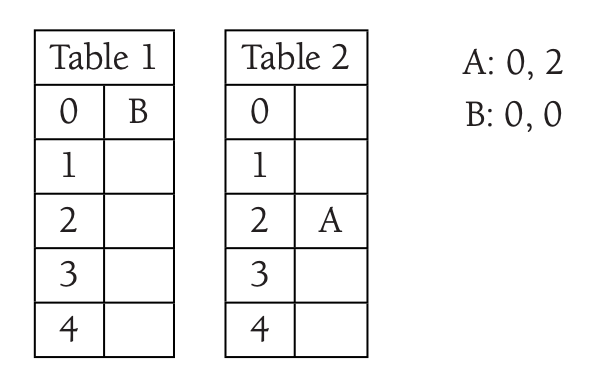
After inserting \(B\) it takes the index 0 in \(T_1\) and move A in \(T_2\).
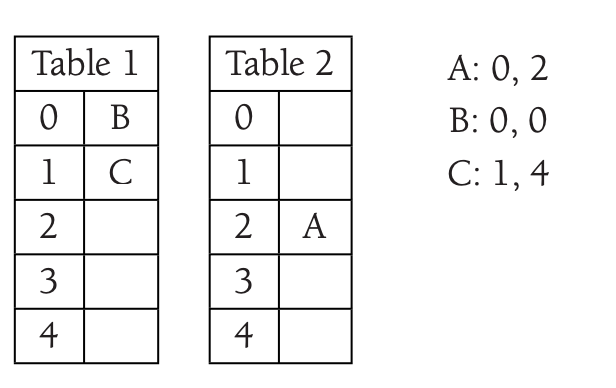
We are inserting \(C\) without collision.
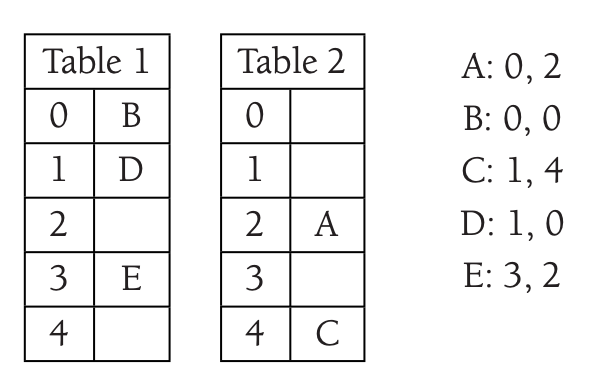
We are inserting \(D\) that collide with \(C\), then we are inserting \(E\).
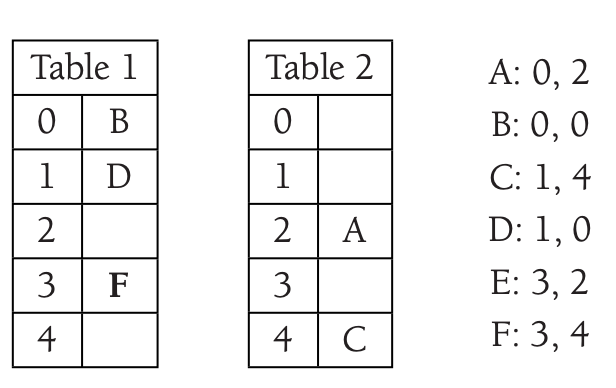
When inserting \(F\) it collides with \(E\).
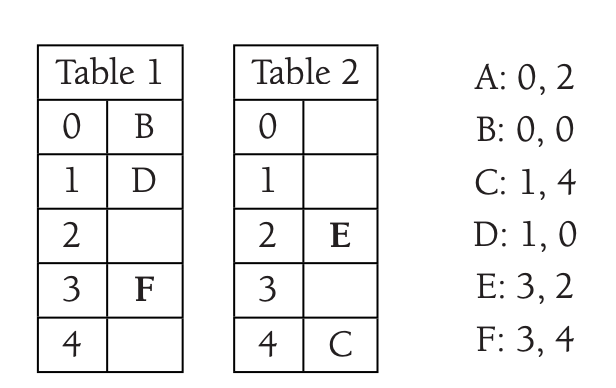
We move \(E\) where \(A\) is.
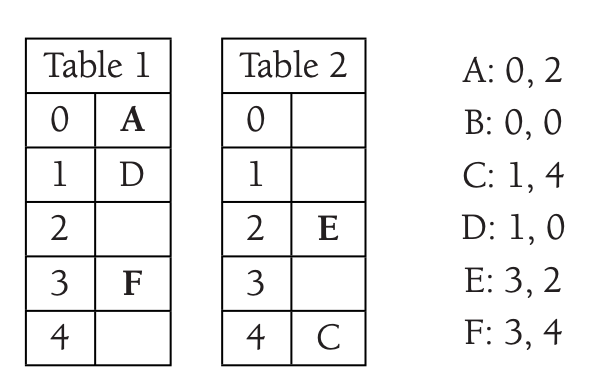
It moves \(A\) to the position of \(B\).
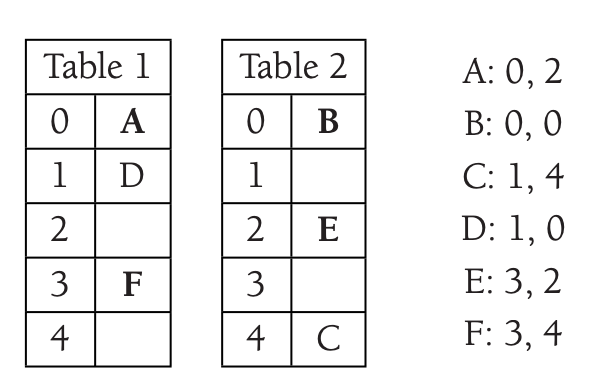
Finally, we move \(B\) to \(T_2\).
There is one issue with this strategy.
If the load of the tables is too important, it could create a cycle.
So when inserting, it is important to rehash the tables when they reach a specific load.
Warning
Cuckoo hashing is extremely sensitive to the choice of hash functions.