Topic 4 - AVL Trees

The classic binary search tree can be unbalanced, reducing the efficiency of the operations on it.

An AVL (Adelson-Velskii and Landis) tree is a binary search tree with a balance condition.

We want to maintain a depth of \(O(\log N)\).

We can enforce some conditions:

1. Requiring that the left subtree has the same depth as the right subtree.

2. Or requiring that every node must have the left and right subtree of the same height.

With the first condition it is not enough, because we can obtain the following tree:

The second condition would work only for trees of \(2^k -1\), otherwise some nodes would be unbalanced. So this condition is too restrictive.

So what are the conditions of the AVL trees?

AVL tree

In AVL trees, for every node in the tree, the height of the left and right subtrees can differ by at most 1.

Note

The height of an empty tree is defined to be -1.

The following figure illustrates the difference between an AVL tree and a binary search tree:

The tree on left is an AVL tree, not the other one.

How does it work?

The height information is kept for each node (in the node structure).

All the operations can be performed in \(O(\log N)\), with the exception of insertion and deletion.

If we take the AVL tree in the previous figure and we try to insert 6, it would destroy the balance condition.

In this case, the property has to be restored before the insertion step is considered over.

To restore the property, we just need to do a rotation.

After an insertion, only nodes that are on the path from the insertion point to the root might have their balance altered because only those nodes have their subtrees altered.

Let us call the node that must be rebalanced \(\alpha\).

Since any node has at most two children, and a height imbalance requires that \(\alpha\)’s two subtrees’ height differs by two, a violation might occur in four cases:

1. An insertion into the left subtree of the left child of \(\alpha\).

2. An insertion into the right subtree of the left child of \(\alpha\).

3. An insertion into the left subtree of the right child of \(\alpha\).

4. An insertion into the right subtree of the right child of \(\alpha\).

Activity

Which node is \(\alpha\) in the previous example?

And in which case, are we?

Cases 1 and 4 are identical in theory, as are cases 2 and 3.

For cases 1 and 4, the insertion occurs on the “outside” (left-left, right-right) and can be fixed by a single rotation.

For cases 2 and 3, the insertion occurs on the “inside” (left-right, right-left) and need to be fixed using a double rotation.

Important

These are fundamental operations! They will be used regularly, so they need to be efficient.

Single Rotation

To illustrate the idea of a single rotation we will consider the following figure.

On the left we have an unbalanced tree after an insertion, and on the right we have the tree after the single rotation.

In detail we have \(k_2\), for which the left subtree is two levels deeper than its right subtree.

The node on the path of the unbalance is \(k_1\).

The idea behind the rotation:

• Imagine that the tree is flexible.

• Grab the node on the path (\(k_1\) in the example).

• Shake it, and let the gravity take hold.

The result will be that \(k_1\) is the new root.

The binary search tree property tells us that in the original tree \(k_2 > k_1\), so \(k_2\) becomes the right child of \(k_1\).

You can also see that \(X, Y\) and \(Z\) are still on the same side respectively to \(k_1\) and \(k_2\).

Note

We could have the symmetric case and it would not change the idea.

Example

Taking back the example of inserting 6 into the AVL tree.

• The node containing 8 is unbalanced.

• The node on the path is 7.

• We rotate 7 and 8.

• We obtain the new subtree with 7 as the root.

Activity

• Consider an empty AVL tree.

• Now, consider the following insertion order: 3,2,1,4,5,6,7.

• Draw the tree after each insertion with the corresponding rotations when necessary.

Solution

• Nothing happens until we try to insert 1.

• When 1 is inserted, the tree becomes unbalanced, so we apply one rotation.

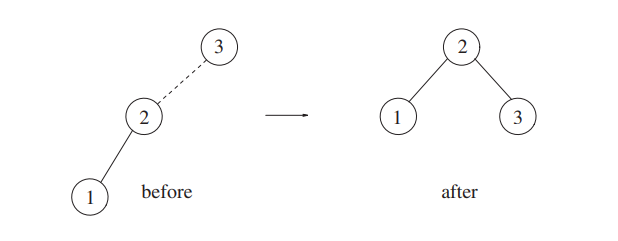
• Then we insert 4.

• When we insert 5, the tree becomes unbalanced.

• We fix it with a rotation.

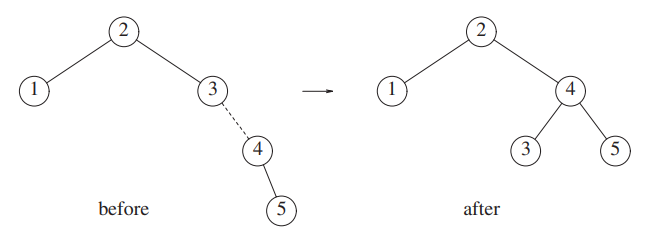
• Then we insert 6.

• The unbalance is at the node 2, so we take the first node on the path between 2 and 6.

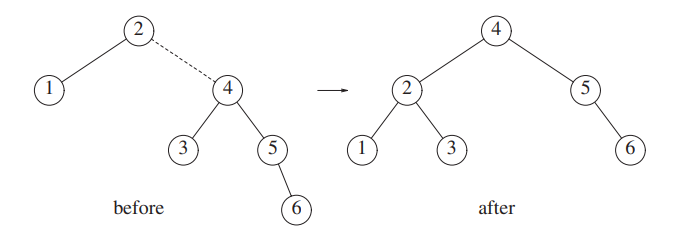
• Finally, we insert 7.

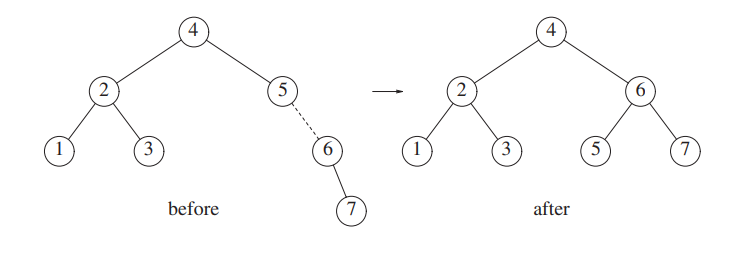
• The node containing 5 becomes unbalanced. 6 is the node on the path, so we rotate 5 and 6.

Double rotation

Using a simple rotation fix cases 1 and 4.

However, it doesn’t work for cases 2 and 3, as shown in the following figure.

The problem is that \(Y\) is too deep and a single rotation does not make it any less deep.

This is why we use a double rotation.

Before using it, we need to consider one more node.

We just inserted a new node in \(Y\), so it’s not empty.

We can consider it has a root and two subtrees.

Consequently, the entire tree may be viewed as four subtrees connected by three nodes.

On which we can apply the double rotation, as illustrated below.

One of the subtree (\(B\) or \(C\)) is deeper than \(D\), but we cannot be sure which one.

In the end, it doesn’t matter, both subtrees are drawn at \(1.5\) levels below \(D\).

Ok, how do balance the tree?

Remember that a rotation between \(k_1\) and \(k_3\) doesn’t work.

So the only root possible is \(k_2\).

It means that \(k_1\) must be the left child of \(k_2\), and \(k_3\) the right child.

Then, we adjust the subtrees:

• \(B\) must be on the left of \(k_2\), so a child of \(k_1\).

• \(C\) must be on the right of \(k_2\), so a child of \(k_3\).

Is is called a double rotation, because it is the same effect of rotating between \(\alpha\)’s child and grandchild, and then between \(\alpha\) and its new child.

Activity

• Take the tree the previous activity (the state after all the insertion).

• Insert the following nodes: 16, 15, 14, 13, 12, 11, 10, 8, 9.

• Draw each step with the corresponding single and double rotations.

Solution

• Adding 16 doesn’t break the balancing.

• However adding 15 does. You can see that 15 is in the interior, so we need to do a double rotation.

• We rotate 16 and 15, then 15 and 7.

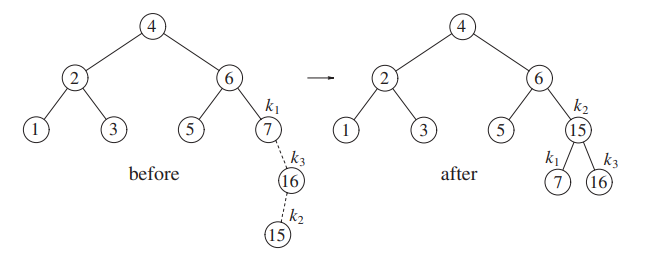
• Next we insert 14, creating a balance issue at node 6.

• We rotate first 7 and 15, then 7 and 6.

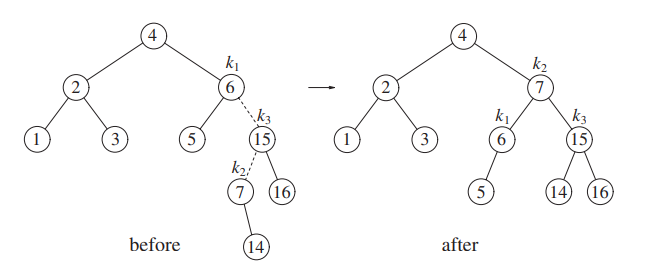
• Now, we insert 13.

• 13 is in the right subtree of the right subtree, so a single rotation is needed.

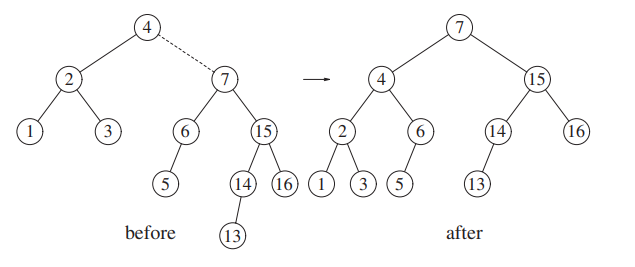
• After inserting 12, we need to balance the tree.

• If you look at it, 12 is in a left-left subtree, so only one rotation is needed.

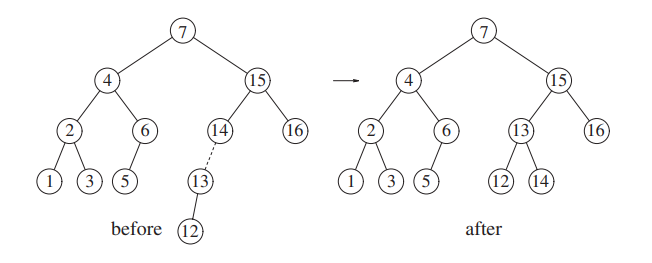
• Inserting 11, and 10 ask for a single rotation each time.

• Inserting 8 doesn’t require any rotation.

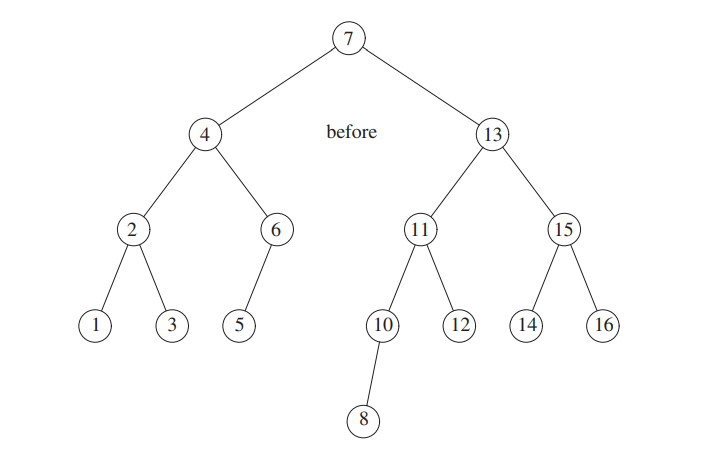
• However inserting 9 makes the tree unbalanced again, since 9 is between 10 and 8.

• We perform a double rotation.

• We roatate 8 and 9, then between 9 and 10.

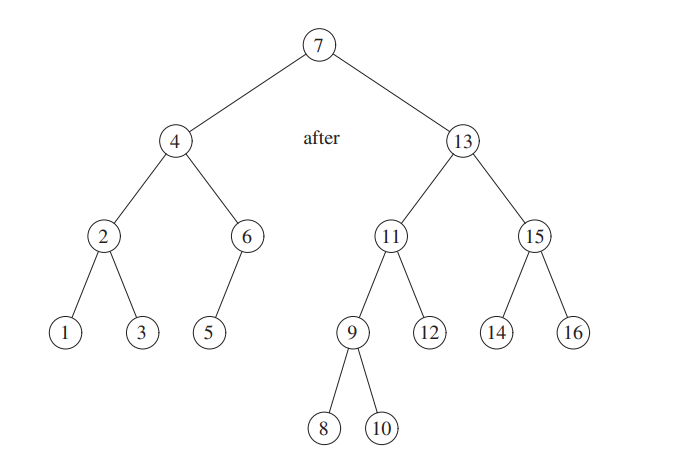
The theory should be clear by now, so we can move to the implementation details.

Implementation of the AVL ADT

The implementation details are straightforward except that there are several cases.

Classes

AVL node

The class representing a node is similar to the one for the binary search tree, but we had the height in it.

    struct AvlNode
    {
        Comparable element;
        AvlNode   *left;
        AvlNode   *right;
        int       height;

        AvlNode( const Comparable & ele, AvlNode *lt, AvlNode *rt, int h = 0 )
          : element{ ele }, left{ lt }, right{ rt }, height{ h } { }
        
        AvlNode( Comparable && ele, AvlNode *lt, AvlNode *rt, int h = 0 )
          : element{ std::move( ele ) }, left{ lt }, right{ rt }, height{ h } { }
    };

As you can see, we keep the type Comparable.

One more thing, we could optimize the type of height and just maintain if one subtree is unbalanced with -1, +1 or 0 if it’s balanced.

However, it complicates the code for a gain that is not that significant.

AVL Tree

For the tree the public interface is the same. In the end what changes is the balancing of the binary tree search.

Something that the user will not need to use directly, so it will be in the private part of the class.

template <typename Comparable>
class AvlTree
{
  public:
    AvlTree( );
    
    AvlTree( const AvlTree & rhs );

    AvlTree( AvlTree && rhs );
    
    ~AvlTree( );

    AvlTree & operator=( const AvlTree & rhs );
        
    AvlTree & operator=( AvlTree && rhs );

    const Comparable & findMin( ) const;

    const Comparable & findMax( ) const;

    bool contains( const Comparable & x ) const;

    bool isEmpty( ) const;

    void printTree( ) const;


    void makeEmpty( );

    void insert( const Comparable & x );
     
    void insert( Comparable && x );

    void remove( const Comparable & x );

  private:
    AvlNode *root;
};

Insertion

To insert a new node containing \(X\) into the tree \(T\):

• Recursively insert \(X\) into the appropriate subtree of \(T\), noted \(T_{LR}\).

• If the height of \(T_{LR}\) doesn’t change, do nothing.

• Otherwise, if a height imbalance appears in \(T\)

  • Apply single or double rotation.

  • Update the heights.

Height

So we need a private method to calculate the height.

Remember that we just need to check the value store in the node we are interested in.

If the node is empty, we return -1.

Activity

• Implement the following function.

    int height( AvlNode *t ) const;

Insert

We could optimize in depth the code of the AVl tree, but it will make ti very unreadable.

So to simplify our life, we will consider two functions:

• The insert function

• And the balance function

The insert one is identical to the one in the binary tree search, except for the private one in which we need to launch the balance after the insertion.

/**
 * Internal method to insert into a subtree.
 * x is the item to insert.
 * t is the node that roots the subtree.
 * Set the new root of the subtree.
 */
void AvlTree::insert( const Comparable & x, AvlNode * & t )
{
    if( t == nullptr )
        t = new AvlNode{ x, nullptr, nullptr };
    else if( x < t->element )
        insert( x, t->left );
    else if( t->element < x )
        insert( x, t->right );
    
    balance( t );
}

This way the balancing will be done at each level, if necessary.

Balance

We need to consider different cases:

• The node is empty; Do nothing;

• The difference between the left subtree and the right subtree is greater than 1.

  • Check if the depth is greater on the exterior (left-left)

    • Simple rotation on the left.

  • Otherwise, double rotation on the left.

• Otherwise, check the difference between the right subtree and the left subtree is greater than 1.

  • Check if the depth is greater on the exterior (right-right).

    • Simple rotation on the right.

  • Otherwise double rotation on the right.

We will use 4 private methods for the rotations:

    void rotateWithLeftChild( AvlNode * & k2 );

    void rotateWithRightChild( AvlNode * & k1 );

    void doubleWithLeftChild( AvlNode * & k3 );

    void doubleWithRightChild( AvlNode * & k1 );

Activity

• Implement the balance method.

// Assume t is balanced or within one of being balanced
void AvlTree::balance( AvlNode * & t )
{
}

Rotations

Starting with void rotateWithLeftChild( AvlNode * & k2 );.

The following figure illustrates the idea.

Simply put, converts the tree on the left to the tree on the right, returning a pointer to the new root. Don’t forget to update the height.

/**
 * Rotate binary tree node with left child.
 * For AVL trees, this is a single rotation for case 1.
 * Update heights, then set new root.
 */
void AvlTree::rotateWithLeftChild( AvlNode * & k2 )
{
    AvlNode *k1 = k2->left;
    k2->left = k1->right;
    k1->right = k2;
    k2->height = max( height( k2->left ), height( k2->right ) ) + 1;
    k1->height = max( height( k1->left ), k2->height ) + 1;
    k2 = k1;
}

Activity

• Implement void rotateWithRightChild( AvlNode * & k1 );

• It’s the symmetric function.

With these functions, the double rotations are simple.

/**
 * Double rotate binary tree node: first left child.
 * with its right child; then node k3 with new left child.
 * For AVL trees, this is a double rotation for case 2.
 * Update heights, then set new root.
 */
void AvlTree::doubleWithLeftChild( AvlNode * & k3 )
{
    rotateWithRightChild( k3->left );
    rotateWithLeftChild( k3 );
}

/**
 * Double rotate binary tree node: first right child.
 * with its left child; then node k1 with new right child.
 * For AVL trees, this is a double rotation for case 3.
 * Update heights, then set new root.
 */
void AvlTree::doubleWithRightChild( AvlNode * & k1 )
{
    rotateWithLeftChild( k1->right );
    rotateWithRightChild( k1 );
}

This what we are doing:

Deletion

We didn’t talk about removing a node.

Again it is the same as for the binary tree search, but we need to balance the tree after each deletion.

/**
 * Internal method to remove from a subtree.
 * x is the item to remove.
 * t is the node that roots the subtree.
 * Set the new root of the subtree.
 */
void AvlTree::remove( const Comparable & x, AvlNode * & t )
{
    if( t == nullptr )
        return;   // Item not found; do nothing
    
    if( x < t->element )
        remove( x, t->left );
    else if( t->element < x )
        remove( x, t->right );
    else if( t->left != nullptr && t->right != nullptr ) // Two children
    {
        t->element = findMin( t->right )->element;
        remove( t->element, t->right );
    }
    else
    {
        AvlNode *oldNode = t;
        t = ( t->left != nullptr ) ? t->left : t->right;
        delete oldNode;
    }
    
    balance( t );
}

Other operations

Everything else is exactly the same as in the binary tree search ADT.

And it should not surprise you.

The AVL Tree is just a self-balancing BST, nothing more, nothing less.