Topic 6 - Red-Black Tree
A popular alternative to the AVL tree is the red-black tree.
The popularity of this BST comes from the fact that each operation take \(O(\log N)\) time in the worst-case.
An added bonus is that it is easy to implement a nonrecursive insertion function.
How is it different from another BST?
A red-black tree is a BST with the following coloring properties:
Every node is colored either red or black.
The root is black.
If a node is red, its children must be black.
Every path from a node to a null pointer must contain the same number of black nodes.
These rules ensure that the height of a red-black tree is at most \(2\log (N+1)\).
The direct consequence is that searching is guaranteed to be a logarithmic operation.
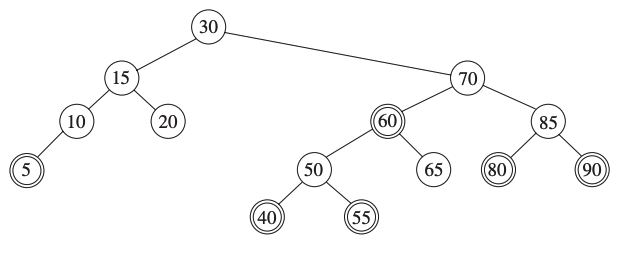
The following figure represents a red-black tree. The red nodes are shown with double circles.
Activity
Check that each property is respected.
What happens if we insert a new node?
Red-black tree will be similar in terms of structure to a BST with some modifications:
1template <typename Comparable>
2class RedBlackTree
3{
4 public:
5 private:
6 enum { RED, BLACK };
7
8 struct RedBlackNode
9 {
10 Comparable element;
11 RedBlackNode *left;
12 RedBlackNode *right;
13 int color;
14 };
15
16 RedBlackNode *header; // The tree header (contains negInf)
17};
18
19#endif
Bottom-Up Insertion
We can see that inserting a new node in the tree is not simple.
There are different cases that we need to consider.
We can take the figure to illustrate the different cases:
If the new node is colored in black.
It violates condition 4. A path will have more black nodes.
It needs to be colored in red.
If it is colored in red.
If the parent is black. We are done.
If the parent is red.
It will violate condition 3.
We need to adjust the tree to ensure condition 3 is enforced.
Basically, we need to focus on the cases in which the parent is red.
Parent is Red
Consider the following:
Let \(X\) be the new node.
Let \(P\) be the parent.
Let \(S\) be the sibling (if it exists).
Let \(G\) being the grandparent.
Only \(X\) and \(P\) are red.
\(G\) is black otherwise there would be two consecutive red nodes prior to the insertion, thus violating the red-black rules.
We will adopt the Splay tree terminology to describe the potential cases:
It can form a zig-zig chain.
Or a zig-zag chain.
Leading to the following figures
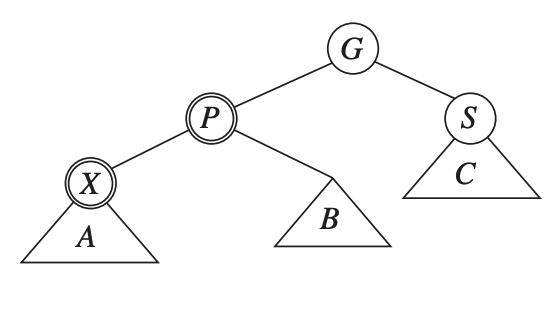
The zig-zig chain
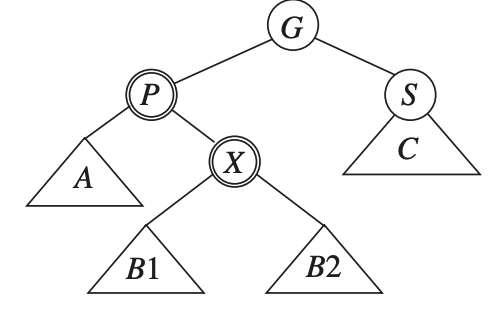
The zig-zag chain
Note
Don’t forget there are the symmetric cases.
Obviously, if we use the same terminology to the Splay trees, we can use the same methods:
Single rotation or zig rotation.
Double rotation or zig-zag rotation.
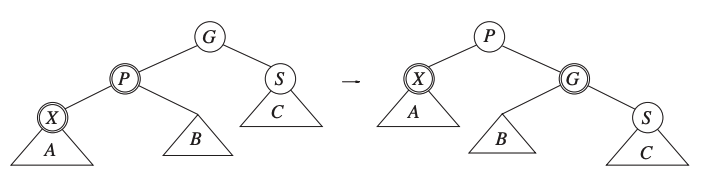
Zig rotation
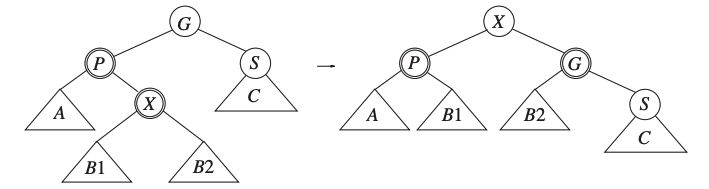
Zig-zag rotation
Activity
Do you find any difference with the Splay trees single and double rotation?
Do you find a pattern with the node coloring and the rotations?
What happens if \(S\) is red?
Insert 79 in the previous example and draw the new tree.
If \(G\) is also red, then we need to apply the change up to the root. We call it percolation.
Top-Down Red-Black Trees
Implementing the percolation is complicated.
It requires to maintain the path using a stack or parent links.
To simplify the insertion, we can apply a Top-Down strategy.
If a node \(X\) has two red children, we make it red and the two children black.
It only creates a violation only if \(X\)’s parent \(P\) is red. In this case we apply a rotation.
Activity
Apply the top-down strategy to insert 45 in the following example.
Draw the tree after each step.

Red-black trees are most of the time very well balanced.
Experiments suggest that the average red-black tree is as deep as an average AVL tree.
Consequently the searching times are typically near optimal.
Implementation
With what we saw, we need to add more internal variables:
1template <typename Comparable>
2class RedBlackTree
3{
4 public:
5 private:
6 enum { RED, BLACK };
7
8 struct RedBlackNode
9 {
10 Comparable element;
11 RedBlackNode *left;
12 RedBlackNode *right;
13 int color;
14 };
15
16 RedBlackNode *header; // The tree header (contains negInf)
17 RedBlackNode *nullNode;
18
19 // Used in insert routine and its helpers (logically static)
20 RedBlackNode *current;
21 RedBlackNode *parent;
22 RedBlackNode *grand;
23 RedBlackNode *great;
24};
25
26#endif
First we need to handle the special case.
We can start by implementing the rotation.
1 /**
2 * Internal routine that performs a single or double rotation.
3 * Because the result is attached to the parent, there are four cases.
4 * Called by handleReorient.
5 * item is the item in handleReorient.
6 * theParent is the parent of the root of the rotated subtree.
7 * Return the root of the rotated subtree.
8 */
9 RedBlackNode * rotate( const Comparable & item, RedBlackNode *theParent )
10 {
11 if( item < theParent->element )
12 {
13 item < theParent->left->element ?
14 rotateWithLeftChild( theParent->left ) : // LL
15 rotateWithRightChild( theParent->left ) ; // LR
16 return theParent->left;
17 }
18 else
19 {
20 item < theParent->right->element ?
21 rotateWithLeftChild( theParent->right ) : // RL
22 rotateWithRightChild( theParent->right ); // RR
23 return theParent->right;
24 }
25 }
Activity
Try to write the pseudocode of the function to handle the special case.
Don’t forget the two cases.
Top-Down Deletion
After insertion, deletion is important too. And as the section suggest it, it can be down with a top-down strategy.
In practice, we need to be able to delete a leaf.
To delete a node \(X\) with two children, we swap it with the smallest node in the right subtree. Then delete it.
Same for a node with only a right child.
To delete a node with only one left child, we find the largest one in the subtree and swap it. Then we delete it.
Deleting a red leaf is trivial.
Important
However, deleting a black node will violate condition 4, so we need to ensure during the top-down pass that the leaf is red.
We start by coloring the root red.
When we arrive at a new node:
We are certain that \(P\) is red,
and \(X\) and \(T\) (the sibling) are black. (We cannot have two consecutive red nodes).
\(T\) has two black children
Then there are 3 subcases.
First case
In this case \(T\) has two black children.
We just need to flip the colors of \(X\), \(T\) and \(P\).
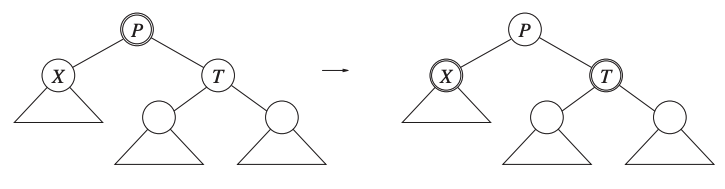
Second Case
The left children of \(T\) is red.
We apply a zig-zag rotation on \(R\).
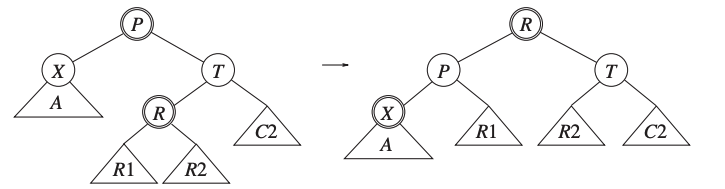
Third Case
The right children of \(T\) is red.
We apply a zig rotation on \(T\).
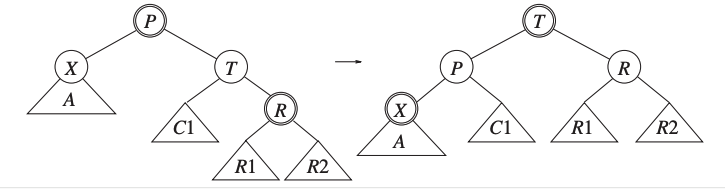
One of \(X\)’s children is red
We go to the next level to obtain new \(X\), \(T\) and \(P\).
If the new \(X\) is the red node, we can continue to the next level.
Otherwise \(T\) is red and \(X\) and \(P\) are black.
We rotate \(T\) and \(P\) making \(X\)’s new parent red.
At this point we can go back to the first main case.