14. A-Star

• We have seen how Dijkstra’s algorithm can help to find the shortest path in a graph.

• However, it requires to visit every node which is time consuming.

• We will now introduce a new concept heuristic search.

14.1. Heuristic search

• Heuristic search is the name given to algorithms that are using a heuristic function to find the solution.

Definition

Heuristic function or heuristic is a function that provides an estimation of the unknown solution.

• Using heuristic functions allow us to prune suboptimal solution, thus saving time.

14.2. A-Star

• The \(A^*\) algorithm was created to solve path planning problem for robots in environments that could contain obstacles.

• It was the first algorithm implementing tree pruning.

• Instead of search in order of closeness from the source, it searches in order of closeness to the goal.

• We had two arrays, \(h[v]\) and \(f[v]\):

  • \(h[v]\) will contain the distance to the node \(v\) calculated by the heuristic function.

  • \(f[v] = d[v]+h[v]\) is the estimated distance from \(s\) to \(v\).

• It selects the node with the smallest \(f\).

14.2.1. How is it working?

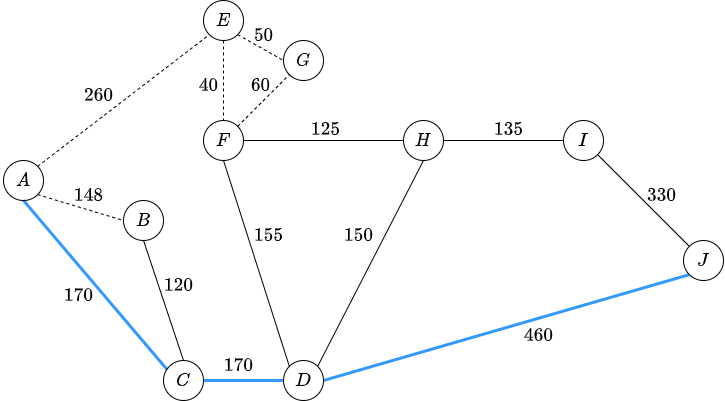
• We will consider the following graph:

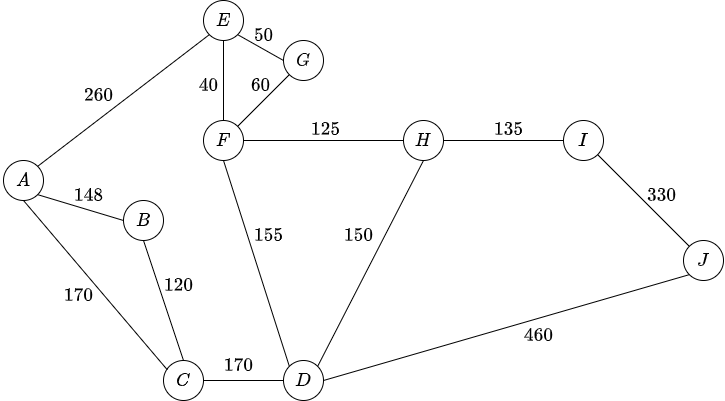
• The source node is \(A\) and the goal is \(J\).

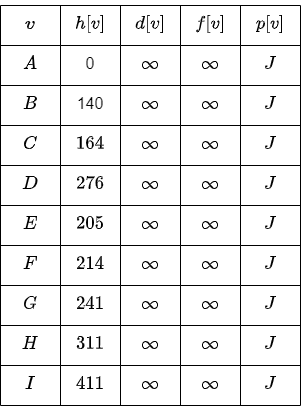
• Using \(A^*\), we will start from \(J\).

• We explores the adjacent edges.

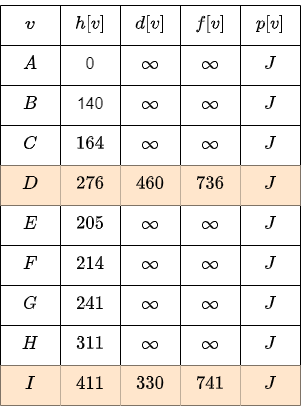
• We visit the closest node \(D\) and explore the adjacent edges.

• The smallest value \(f\) is for the node \(I\).

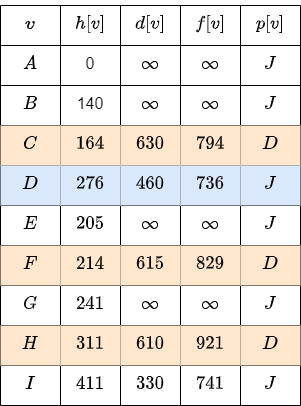
• We visit \(I\) and check the edges.

• We update \(H\), because it’s new value \(465\) is smaller than the previous \(610\).

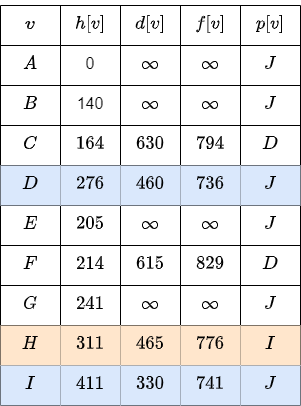
• The smallest value is \(776\) for the node \(H\).

• We visit this node and check the edge leading to \(F\).

• The new value \(590\) is smaller than the previous value \(615\).

• Now, the node with the smallest estimated distance is going through \(C\).

• We are updated the adjacent nodes that are not visited yet, so \(A\) and \(B\).

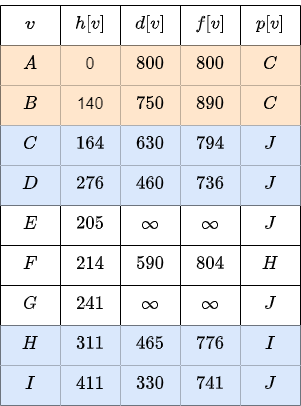
• Since the distance to \(A\) is smallest that the other estimation, we stop.

14.2.2. Algorithm

• Now, we can discuss the pseudocode:

Initialize V–S with all vertices except the starting vertex s.
for all v in V–S:
    p[v] = s
    if there is an edge (s, v):
        d[v] = w(s, v)
        f[v] = d[v] + h(v)
    else:
        d[v] = inf
        f[v] = inf

while V–S is not empty:
    u = find the smallest f[u]
    if u == destination:
        break
    Remove u from V–S
    Add u to S
    for all v adjacent to u in V–S:
        if d[u] + w(u, v) < d[v]:
            d[v] = d[u] + w(u, v)
            f[v] = d[v] + h(v)
            p[v] = u