13. Dijsktra’s Algorithm

13.1. Previously

We introduced graphs.
We covered a single source shortest-path algorithm for unweighted graph \(G = (V, E)\).
The algorithm we covered is Breadth-First-Search (BFS).
The idea:

function BFS(Graph, source):

    Create a queue Q.
    Q.insert(s).

    while Q not empty:
        u = Q.pop()
        visit(u)
        for all v adjacent to u:
            if v not marked or visited:
                Mark v
                Q.insert(v)

We took the following graph as example:

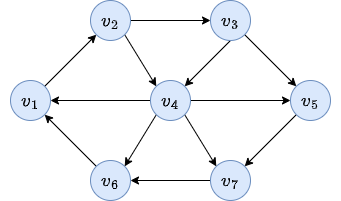
../../_images/unweighted_graph.drawio.png

After applying the algorithm, we obtained:

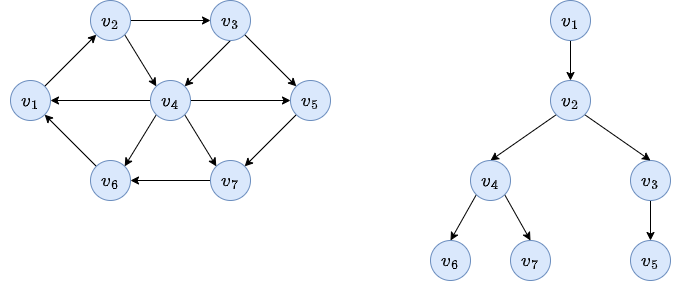
Activity

What happens if the graph has weighted edges?

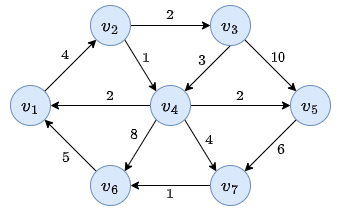
13.2. Dijsktra’s Algorithm

Dijsktra’s algorithm is a single source shortest-path algorithm for weighted graph.
It is also a greedy algorithm, meaning that we always take the closest node not already visited.
To work we need a few assumptions:
- There is a path between the source (or start) and every other node in the graph.
- All edges have a positive weight.

13.2.1. Application

Computer networking
Transportation
Geographic information systems

13.2.2. How is it working?

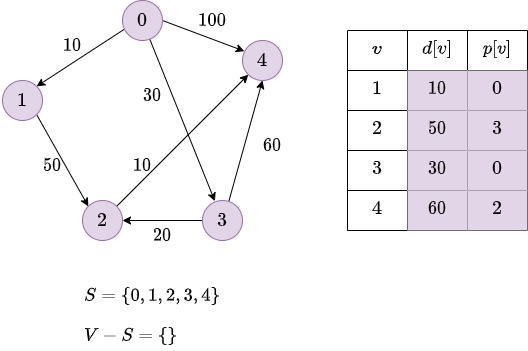
To explain how the algorithm works, we will consider the following graph:

../../_images/weighted_graph.drawio1.png

We consider two sets of nodes \(S\) and \(V-S\).
- \(S\): set of nodes with the shortest distance already computed.
- \(V-S\): set of nodes remaining.
We also need two arrays \(d\) and \(p\):
- \(d[v]\): the shortest distance from \(s\) to \(v\).
- \(p[v]\): the predecessor of \(v\) in the path from \(s\) to \(v\).
We initialize \(S\) with \(0\).
We place every nodes remaining in \(V-S\).
For each adjacent \(v\) of \(s\), we set \(d[v]\) equal to \(w(s, v)\).
The predecessor is \(0\) for every \(v\).

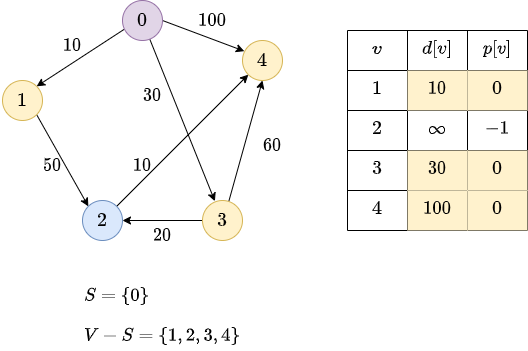
Now we find the vertex (node) \(u \in V-S\) that has the smallest \(d[v]\).
For every node \(v\) adjacent to \(u\):
- if \(d[u] + w(u,v) < d[v]\), we update \(d[v]\).
- and we set \(p[v]\) to \(u\).
In our example:

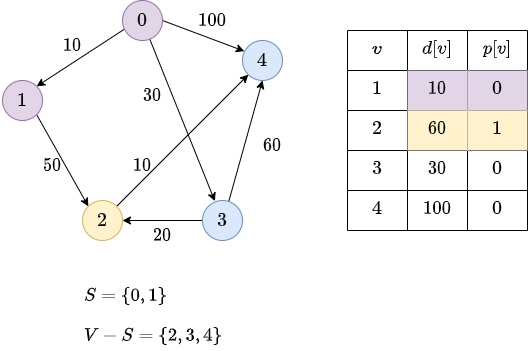
We continue:

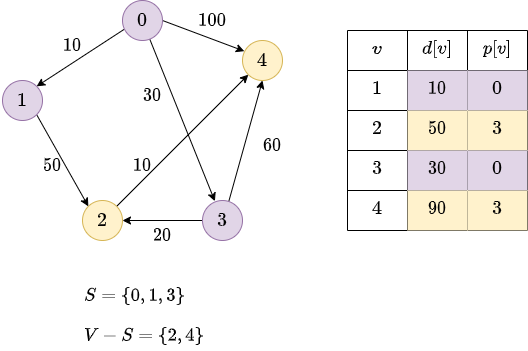
Again:

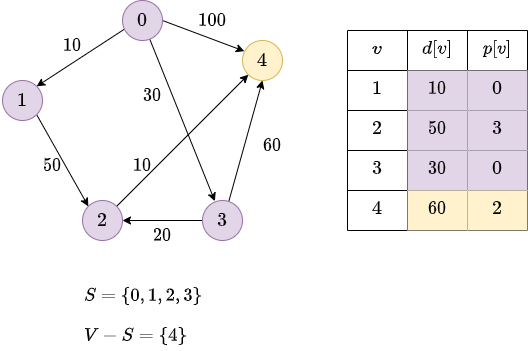
Finally:

13.2.3. Algorithm

Now we can discuss how to implement it.
A straightforward implementation is to use a list to maintain \(V-S\):

function Dijkstra(Graph, source):
    create empty list L
    for all vertex v in G:
        d[v] = infinity
        p[v] = null
        L.insert(v)
    d[source] = 0
    while L is not empty:
        u = vertex in L with smallest d value
        L.remove(u)
        for each neighbor v of u:
            alt = dist[u] + w(u, v)
            if alt < dist[v]:
                d[v] = alt
                p[v] = u

Activity

What is the time complexity of this implementation?

The time complexity if \(O(|V|^2)\):

The initialization takes \(O(|V|)\) as we need to insert every nodes in the list.
The while loop is \(O(|V|)\) as we need to loop over every nodes.
- We have two nested loops inside.
- The first is finding the closest node, so a linear search \(O(|V|)\).
- The second one is checking each adjacent not in \(S\), so \(O(|V|)\).

We can improve this by using a binary heap.

function Dijkstra(Graph, source):
    create empty priority queue Q
    dist[source] = 0
    for each vertex v in Graph:
        if v != source:
            dist[v] = infinity
            p[v] = null
            Q.insert(v, dist[v])
    Q.insert(source, 0)
    while Q is not empty:
        u = Q.extract_min()
        for each neighbor v of u:
            alt = dist[u] + w(u, v)
            if alt < dist[v]:
                dist[v] = alt
                p[v] = u
                Q.decrease_key(v, alt)
    return dist

The initialization is \(O(|V|\log |V|)\).
Q.extract_min() is \(O(\log |V|)\).
Q.decrease_key(v, alt) is \(O(\log |V|)\).
So the loop checking the adjacent nodes is \(O(|E|\log |V|)\).

Important

We visit each edges at most once! Thus the complexity is the complexity of updating all the adjacent nodes \(O(|E|\log |V|)\).

13.2.4. Proof of Correctness

Let \(G = (V, E)\) be a weighted, directed graph, where \(V\) is the set of vertices and \(E\) is the set of edges, and let \(s\) be the source vertex.
Let \(d[v]\) be the current distance estimate from the source vertex \(s\) to vertex \(v\).
We claim:

Claim

Each time Dijkstra’s algorithm selects a path to a node \(v\), that path is shorter than every other path to \(v\).

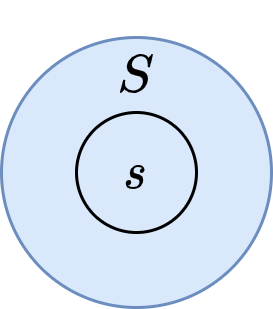
13.2.4.1. Base case

We start with the base case, \(|S| = 1\).
- \(d[s] = 0\) and \(d[v] = +\infty, \forall v \neq s\).
The claim hold for \(S = {s}\).

13.2.4.2. Hold for \(n\)

Suppose the claim hold when \(|S| = n, n \geq 1\).

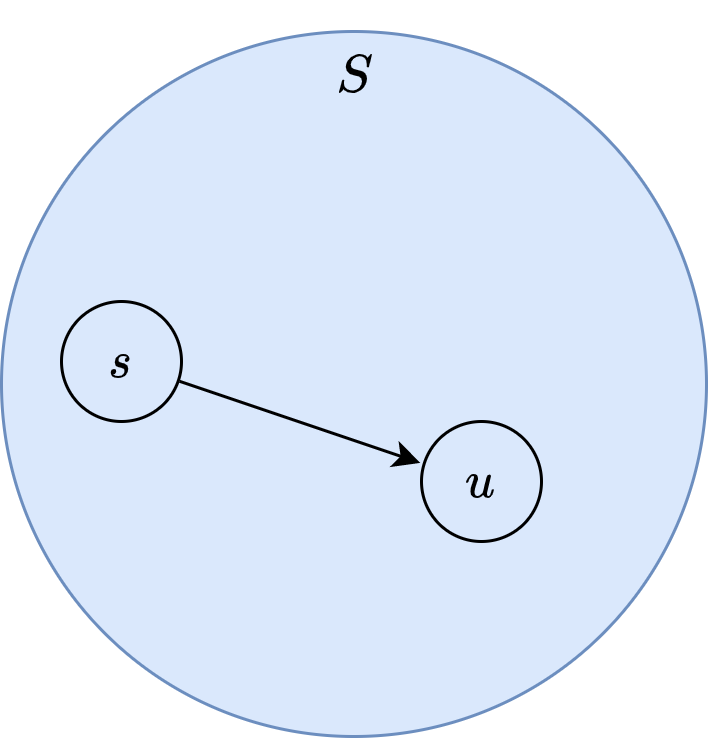
13.2.4.3. Induction step

Dijkstra’s algorithm add one more node \(v\) to \(S\).
- So \(|S| = n+1\).
- let \((u,v)\) the final edge on the path \(s-v\) denoted \(P_v\).
By induction hypothesis \(P_u\) is the shortest path from \(s\) to \(u\).

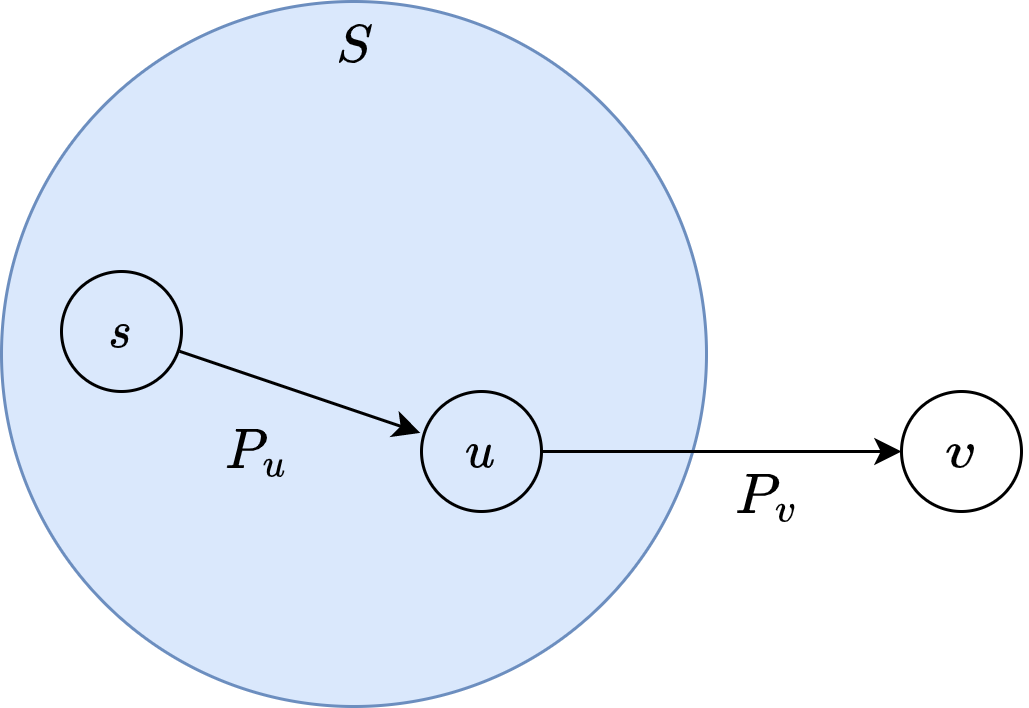
Now, consider any other path \(s-v\), denoted \(P'_v\).
- We want to show that \(P'_v\) is as least as long as \(P_v\).
- \(P'_v\) must leave \(S\) somewhere.

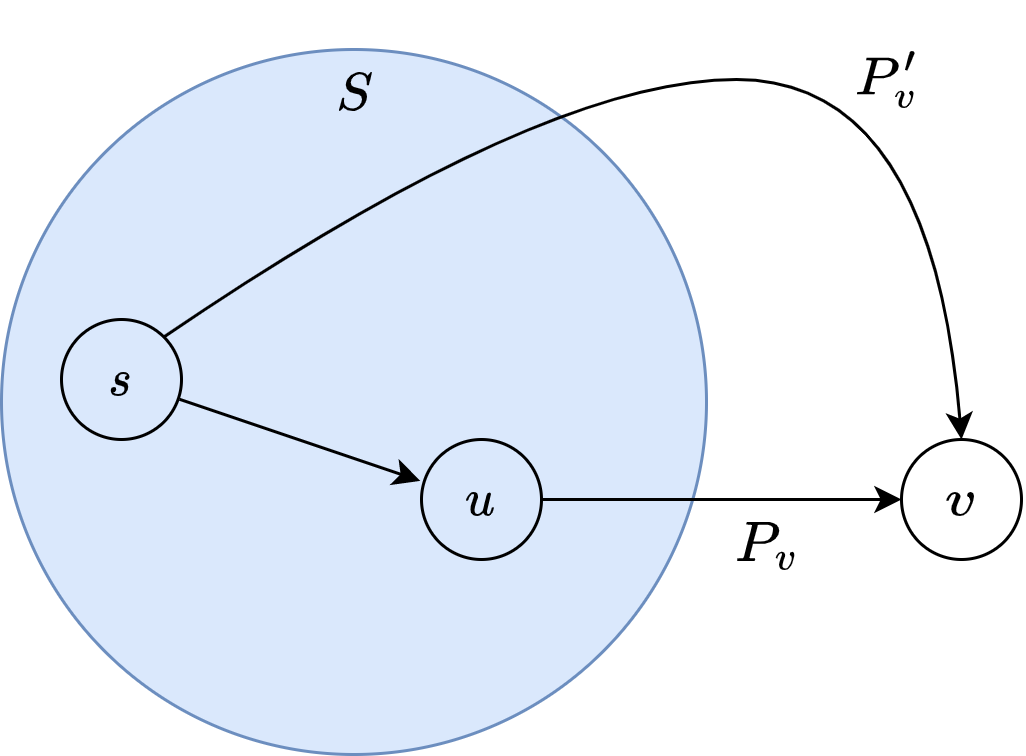
Let denote \(y\) the node on \(P'_v\), but not in \(S\).
Let denote \(x\) the node before \(y\), but in \(S\).

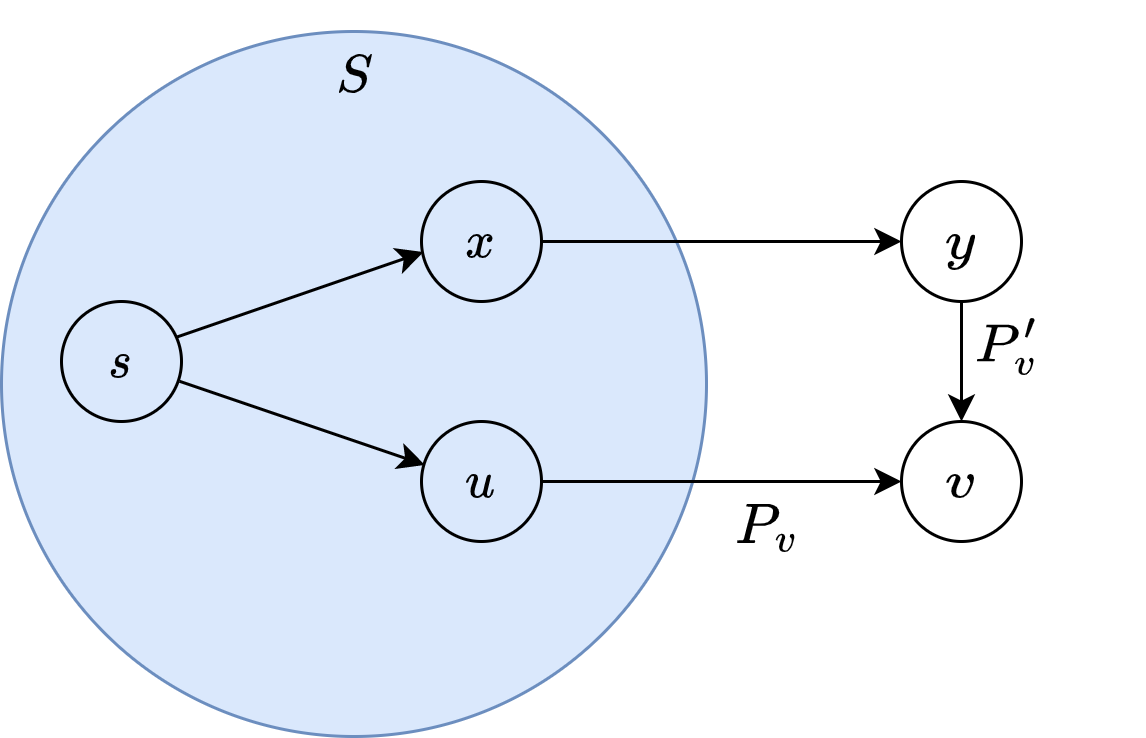
\(P'_v\) cannot be shorter than \(P_v\).
- At iteration \(n+1\), Dijkstra considered \(y\) and rejected it.
- It chose \(v\) instead.
- So there is not path \(s-y\) through \(x\) shorter than \(P_v\).

13.2.5. Negative Weights

Until now, we assume that the graph only has positive weights.
If there are negative weights, then Dijkstra is not optimal.

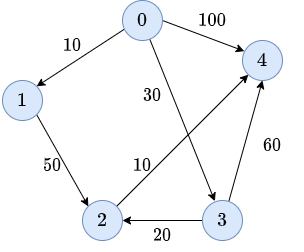
Example

Consider the following example:

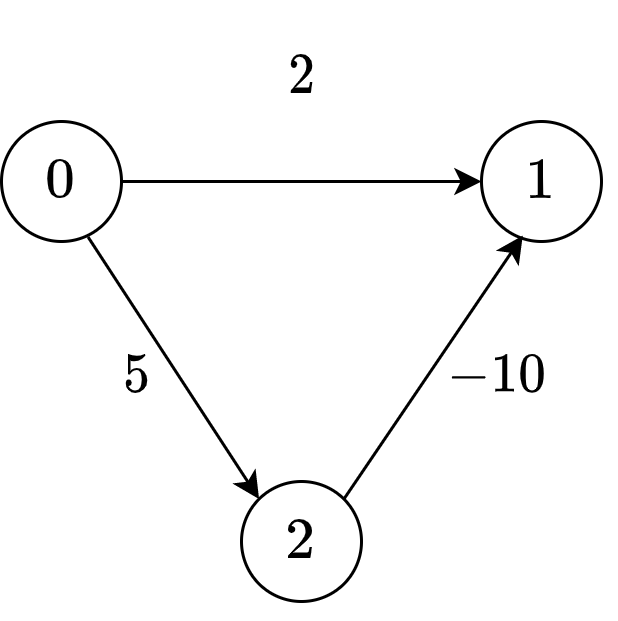
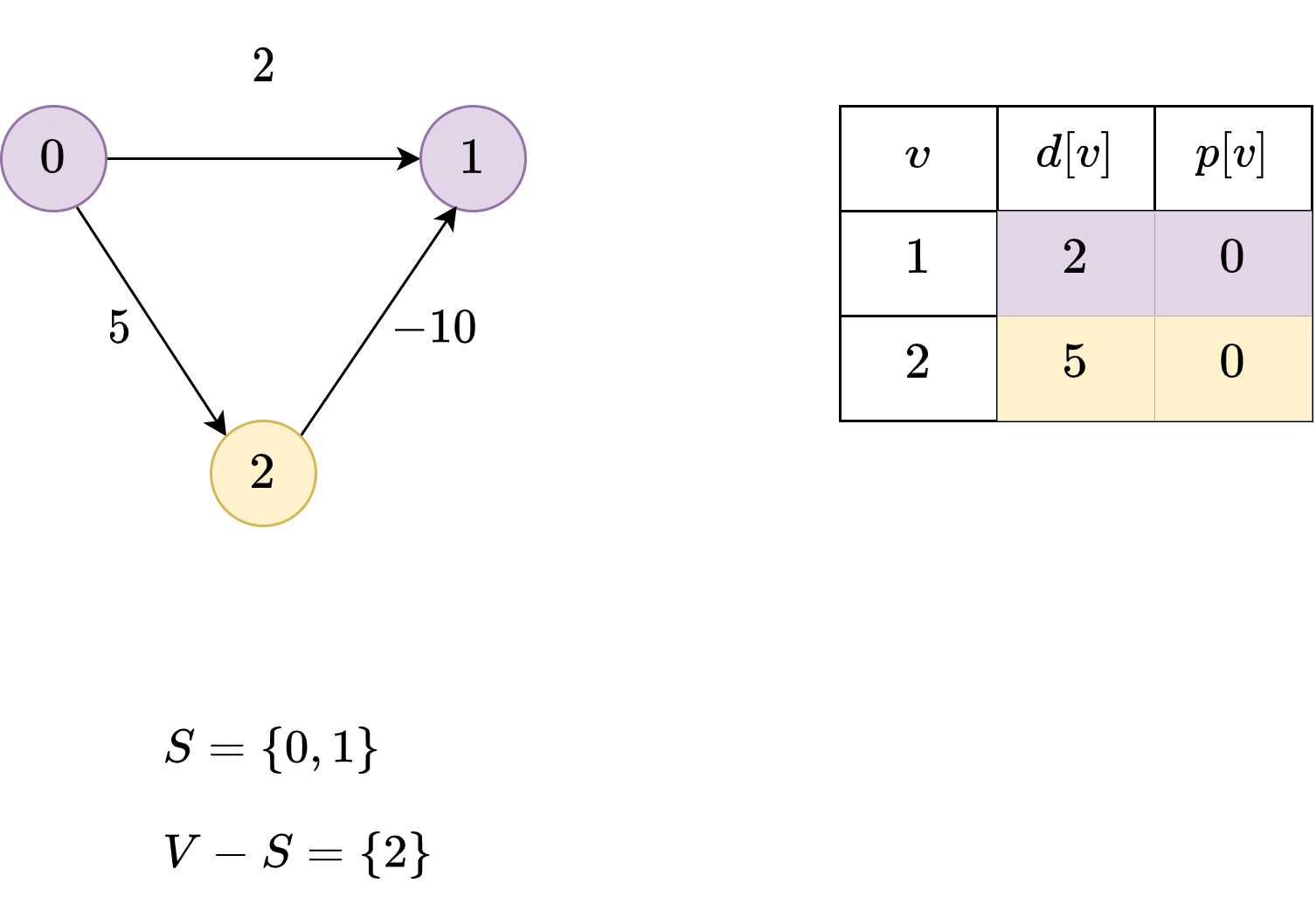
We initialize \(S\) and \(V-S\).
We update \(d[v]\) for every adjacent node of \(s\).

We choose \(1\) and add it to \(S\).
\(1\) has no adjacent nodes in \(V-S\).

We add \(2\) to \(S\).
\(2\) has no adjacent nodes in \(V-S\).
- So, we don’t update \(1\)!

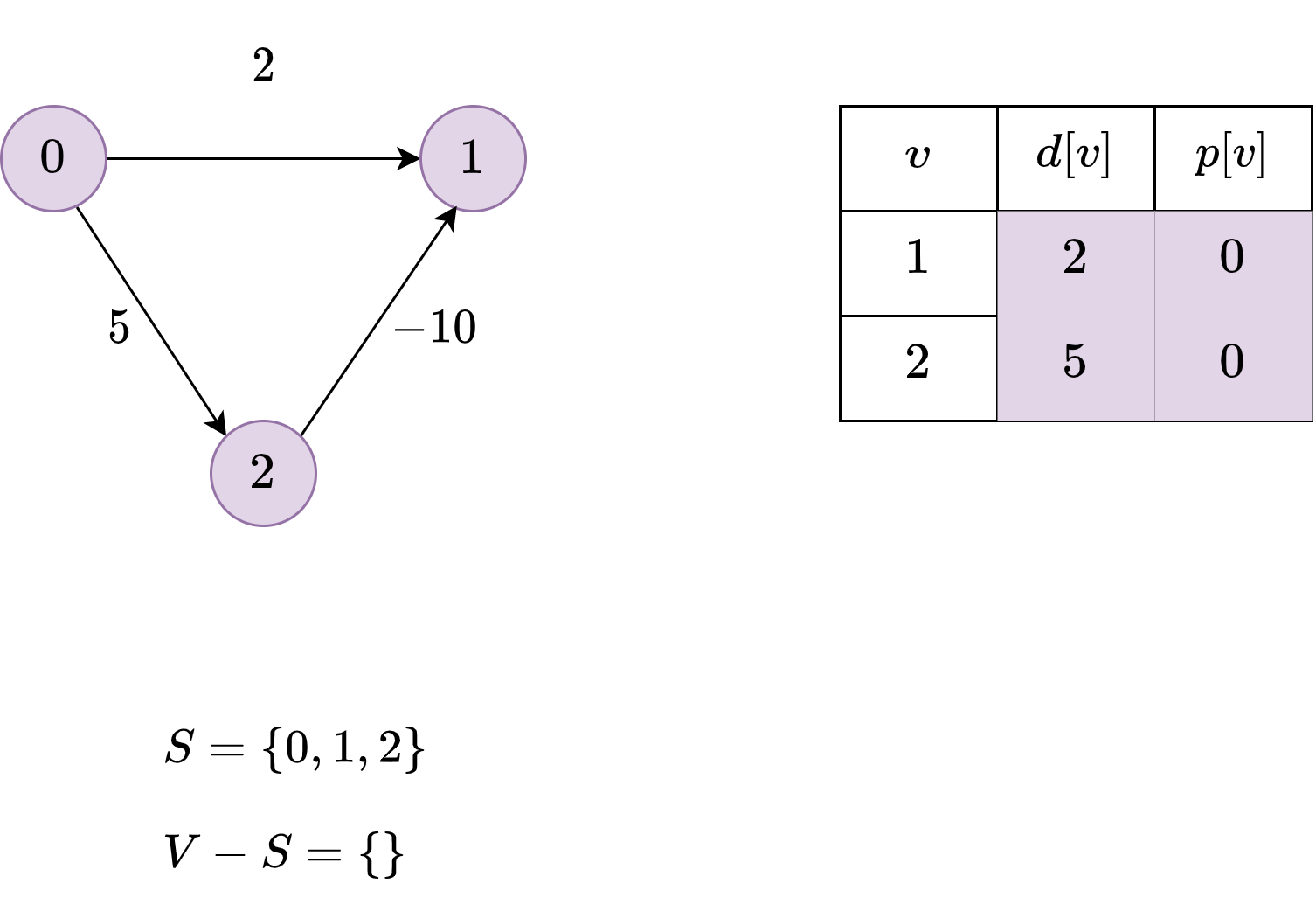
Important

This is why Dijkstra’s algorithm doesn’t work with negative weight.
Once a node is added to \(S\), we consider that we have the shortest distance to it.