15. Network Flow Problems

• Suppose a directed graph \(G=(V,E)\).

• Each edge has a capacity of \(c_{v,w}\).

• We could consider that the capacity is the amount of water that could flow through a pipe.

Definition

• In a network flow problem, the graph contains two nodes:

  • \(s\) called the source.

  • \(t\) called the sink.

• \(c_{v,w}\) is the maximum unit of “flow” that can pass.

• At any vertex \(v\) (not being \(s\) or \(t\)) the total incoming flow must be equal to the total flow exiting the node.

• The maximum flow problem is to determine the maximum flow amount that can pass from \(s\) to \(t\).

• The following graph has a maximum flow of 5:

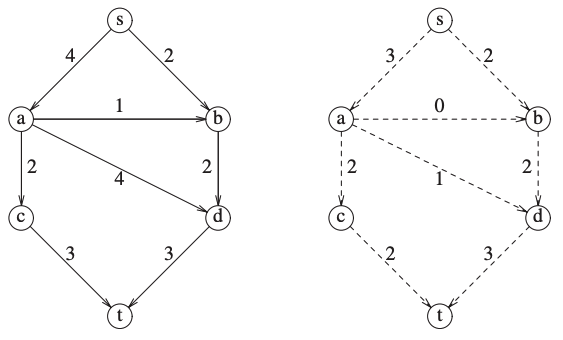
Activity

• Do you have any real application of this problem?

• Can you increase the flow in this graph?

• Can you prove it?

• If we cut the graph in two parts:

  • A part containing \(s\) and few nodes.

  • A part containing \(t\) and few nodes.

• The capacity leaving the first part is the maximum flow:

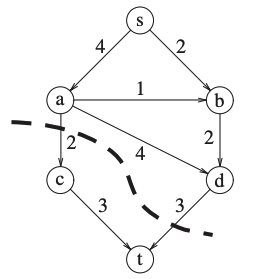
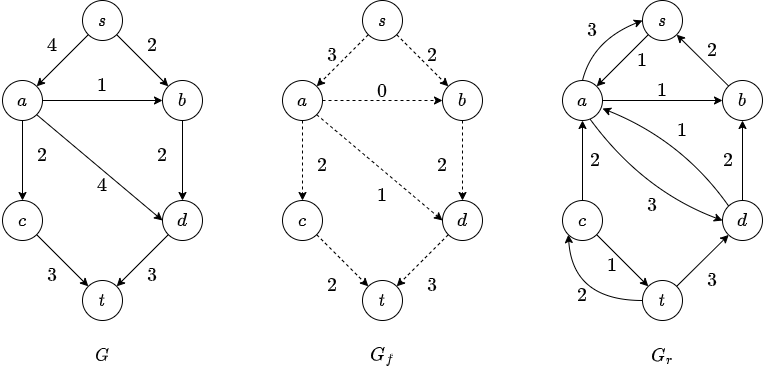
15.1. A simple Maximum-Flow algorithm

• We start with our graph \(G\) and construct a flow graph \(G_f\).

• \(G_f\) is the flow that has been attained at any stage.

• Initially all edges in \(G_f\) has no flow.

• At the end \(G_f\) should contain the maximum flow.

• We also construct \(G_r\), the residual graph.

• \(G_r\) contains for each edge how much flow can be added.

How does it work?

• At each stage, we find a path in \(G_r\) from \(s\) to \(t\).

• The minimum edge on the path is the amount of flow that is added to every edge on the path in \(G_f\).

• We recalculate \(G_r\) and we add an opposite edge with the same capacity.

• When we find no path from \(s\) to \(t\) in \(G_r\) we stop.

Example

• If we apply it to the previous graph.

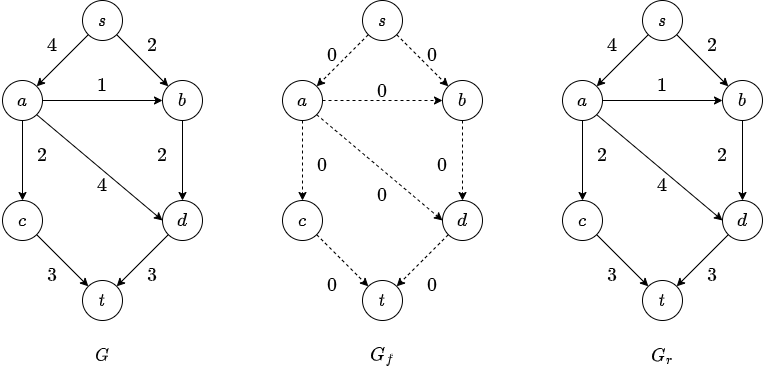
• Now we find a path:

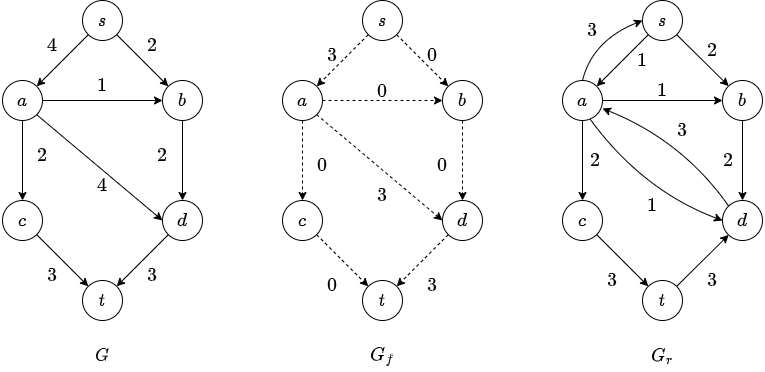
• And we continue:

• You can see that we changed a previous flow.