5. AVL Trees

The classic binary search tree can be unbalanced, reducing the efficiency of the operations on it.

An AVL (Adelson-Velskii and Landis) tree is a binary search tree with a balance condition.

We want to maintain a depth of \(O(\log N)\).

We can enforce some conditions:

1. Requiring that the left subtree has the same depth as the right subtree.

2. Or requiring that every node must have the left and right subtree of the same height.

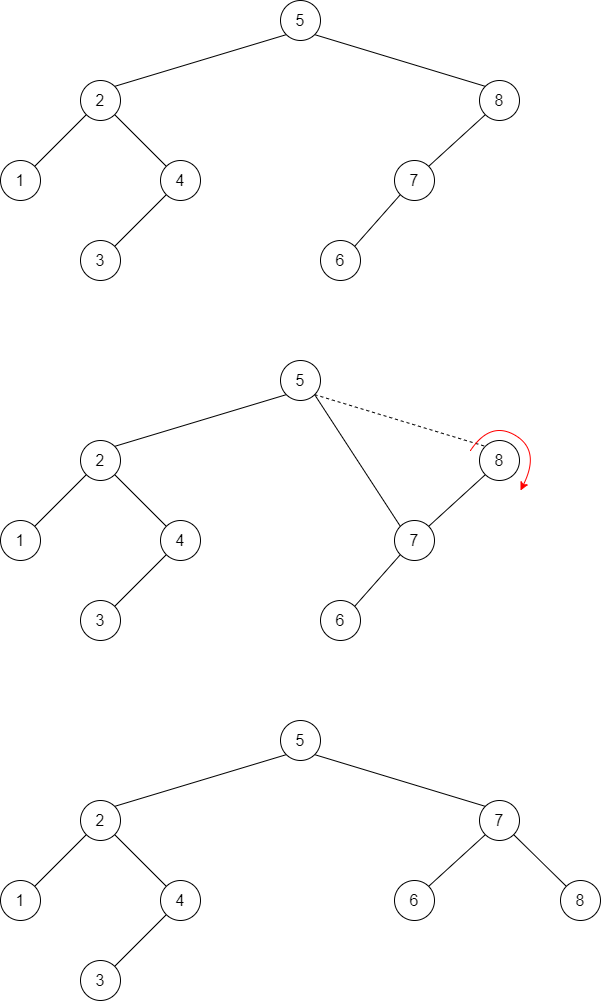
With the first condition it is not enough, because we can obtain the following tree:

The second condition would work only for trees of \(2^k -1\), otherwise some nodes would be unbalanced. So this condition is too restrictive.

So what are the conditions of the AVL trees?

AVL tree

In AVL trees, for every node in the tree, the height of the left and right subtrees can differ by at most 1.

Note

The height of an empty tree is defined to be -1.

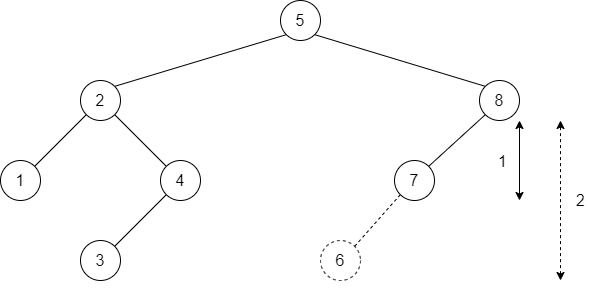
The following figure illustrates the difference between an AVL tree and a binary search tree:

The tree on left is an AVL tree, not the other one.

5.1. How does it work?

The height information is kept for each node (in the node structure).

All the operations can be performed in \(O(\log N)\), with the exception of insertion and deletion.

If we take the AVL tree in the previous figure and we try to insert 6, it would destroy the balance condition.

In this case, the property has to be restored before the insertion step is considered over.

To restore the property, we just need to do a rotation.

After an insertion, only nodes that are on the path from the insertion point to the root might have their balance altered because only those nodes have their subtrees altered.

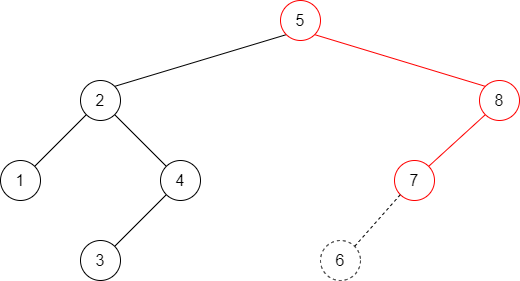
Let us call the node that must be rebalanced \(\alpha\).

Since any node has at most two children, and a height imbalance requires that \(\alpha\)’s two subtrees’ height differs by two, a violation might occur in four cases:

1. An insertion into the left subtree of the left child of \(\alpha\).

2. An insertion into the right subtree of the left child of \(\alpha\).

3. An insertion into the left subtree of the right child of \(\alpha\).

4. An insertion into the right subtree of the right child of \(\alpha\).

Activity

Which node is \(\alpha\) in the previous example?

And in which case, are we?

Cases 1 and 4 are identical in theory, as are cases 2 and 3.

For cases 1 and 4, the insertion occurs on the “outside” (left-left, right-right) and can be fixed by a single rotation.

For cases 2 and 3, the insertion occurs on the “inside” (left-right, right-left) and need to be fixed using a double rotation.

Important

These are fundamental operations! They will be used regularly, so they need to be efficient.

5.2. Single Rotation

To illustrate the idea of a single rotation we will consider the following figure.

On the left we have an unbalanced tree after an insertion, and on the right we have the tree after the single rotation.

In detail we have \(k_2\), for which the left subtree is two levels deeper than its right subtree.

The node on the path of the unbalance is \(k_1\).

The idea behind the rotation:

• Imagine that the tree is flexible.

• Grab the node on the path (\(k_1\) in the example).

• Shake it, and let the gravity take hold.

The result will be that \(k_1\) is the new root.

The binary search tree property tells us that in the original tree \(k_2 > k_1\), so \(k_2\) becomes the right child of \(k_1\).

You can also see that \(X, Y\) and \(Z\) are still on the same side respectively to \(k_1\) and \(k_2\).

Note

We could have the symmetric case and it would not change the idea.

Example

Taking back the example of inserting 6 into the AVL tree.

• The node containing 8 is unbalanced.

• The node on the path is 7.

• We rotate 7 and 8.

• We obtain the new subtree with 7 as the root.

Activity

• Consider an empty AVL tree.

• Now, consider the following insertion order: 3,2,1,4,5,6,7.

• Draw the tree after each insertion with the corresponding rotations when necessary.

Solution

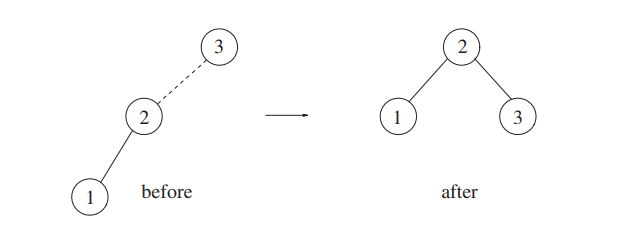
• Nothing happens until we try to insert 1.

• When 1 is inserted, the tree becomes unbalanced, so we apply one rotation.

• Then we insert 4.

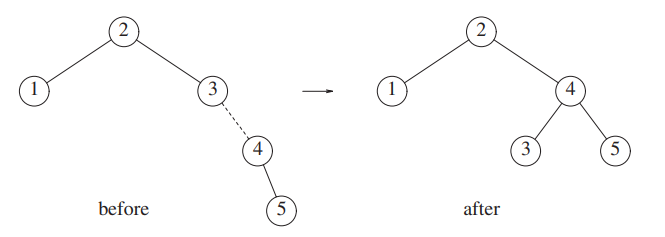
• When we insert 5, the tree becomes unbalanced.

• We fix it with a rotation.

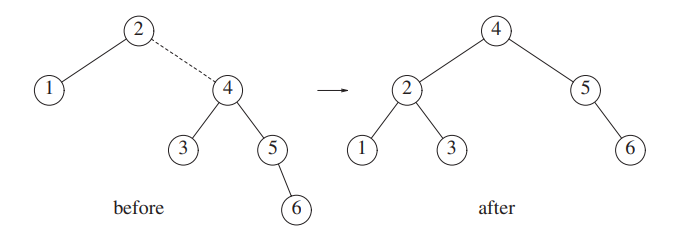
• Then we insert 6.

• The unbalance is at the node 2, so we take the first node on the path between 2 and 6.

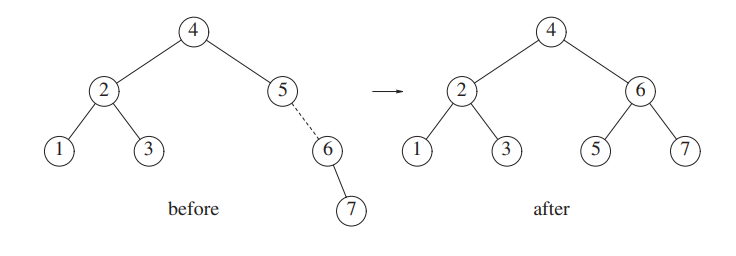
• Finally, we insert 7.

• The node containing 5 becomes unbalanced. 6 is the node on the path, so we rotate 5 and 6.

5.3. Double rotation

Using a simple rotation fix cases 1 and 4.

However, it doesn’t work for cases 2 and 3, as shown in the following figure.

The problem is that \(Y\) is too deep and a single rotation does not make it any less deep.

This is why we use a double rotation.

Before using it, we need to consider one more node.

We just inserted a new node in \(Y\), so it’s not empty.

We can consider it has a root and two subtrees.

Consequently, the entire tree may be viewed as four subtrees connected by three nodes.

On which we can apply the double rotation, as illustrated below.

One of the subtree (\(B\) or \(C\)) is deeper than \(D\), but we cannot be sure which one.

In the end, it doesn’t matter, both subtrees are drawn at \(1.5\) levels below \(D\).

Ok, how do balance the tree?

Remember that a rotation between \(k_1\) and \(k_3\) doesn’t work.

So the only root possible is \(k_2\).

It means that \(k_1\) must be the left child of \(k_2\), and \(k_3\) the right child.

Then, we adjust the subtrees:

• \(B\) must be on the left of \(k_2\), so a child of \(k_1\).

• \(C\) must be on the right of \(k_2\), so a child of \(k_3\).

Is is called a double rotation, because it is the same effect of rotating between \(\alpha\)’s child and grandchild, and then between \(\alpha\) and its new child.

Activity

• Take the tree the previous activity (the state after all the insertion).

• Insert the following nodes: 16, 15, 14, 13, 12, 11, 10, 8, 9.

• Draw each step with the corresponding single and double rotations.

Solution

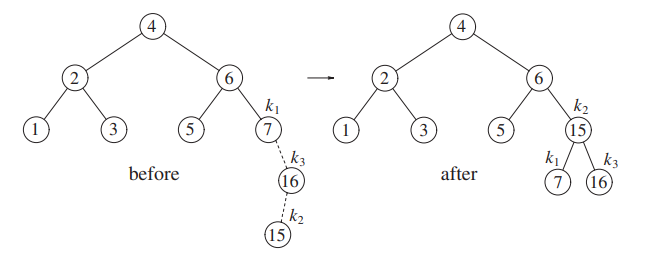
• Adding 16 doesn’t break the balancing.

• However adding 15 does. You can see that 15 is in the interior, so we need to do a double rotation.

• We rotate 16 and 15, then 15 and 7.

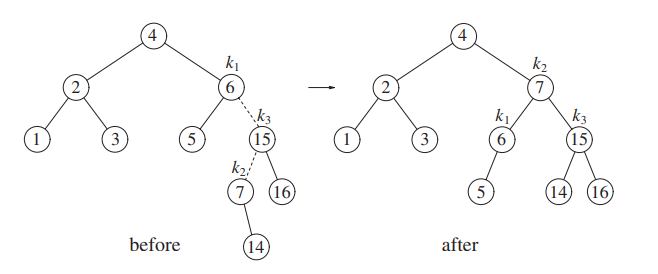
• Next we insert 14, creating a balance issue at node 6.

• We rotate first 7 and 15, then 7 and 6.

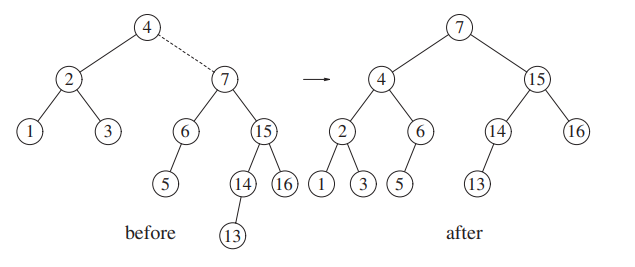
• Now, we insert 13.

• 13 is in the right subtree of the right subtree, so a single rotation is needed.

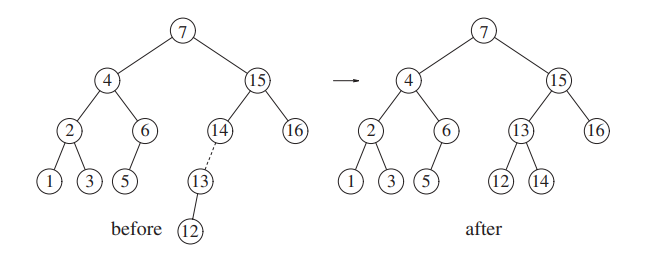
• After inserting 12, we need to balance the tree.

• If you look at it, 12 is in a left-left subtree, so only one rotation is needed.

• Inserting 11, and 10 ask for a single rotation each time.

• Inserting 8 doesn’t require any rotation.

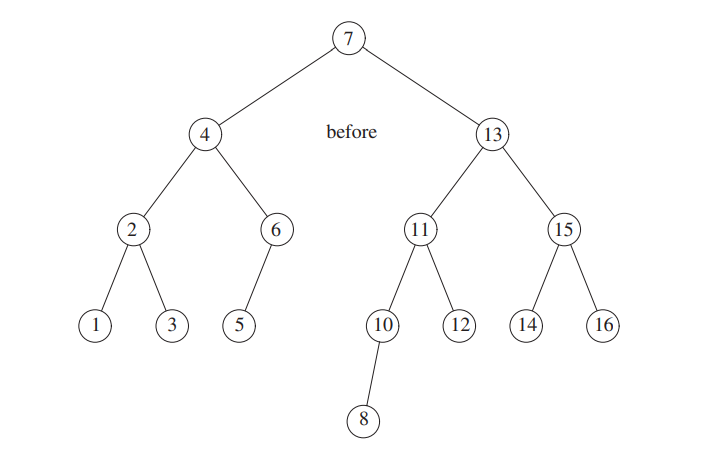
• However inserting 9 makes the tree unbalanced again, since 9 is between 10 and 8.

• We perform a double rotation.

• We roatate 8 and 9, then between 9 and 10.

The theory should be clear by now, so we can move to the implementation details.

5.4. Implementation of the AVL ADT

The implementation details are straightforward except that there are several cases.

5.4.1. Classes

AVL node

The class representing a node is similar to the one for the binary search tree, but we had the balancing in it.

    /**
     * Class to represent an AVL Node.
     * It extends the BinaryTree.Node by adding the balance field.
     * @param <E> Type of the element in the tree.
     */
    private static class AVLNode<E> extends Node<E>{

        /** Constant to indicate left‐heavy */
        public static final int LEFT_HEAVY = -1;
        /** Constant to indicate balanced */
        public static final int BALANCED = 0;
        /** Constant to indicate right‐heavy */
        public static final int RIGHT_HEAVY = 1;
        /** balance is right subtree height – left subtree height */
        private int balance;

        /**
         * Construct a node with the given item as the data field.
         * @param item The data field
         */
        public AVLNode(E item){
            super(item);
            balance = BALANCED;
        }

        /**
         * Return a string representation of this object.
         * The balance value is appended to the contents.
         * @return String representation of this object.
         */
        @Override
        public String toString(){
            return balance + ": " + super.toString();
        }

    }

As you can see, we inherit from Node, so we don’t need to redefine everything.

One more thing, we optimize the type of height and just maintain if one subtree is unbalanced with -1, +1 or 0 if it’s balanced.

However, it complicates the code.

AVL Tree

For the tree the public interface is the same. In the end what changes is the balancing of the binary tree search.

Something that the user will not need to use directly, so it will be in the private part of the class.

/**
 * Self-balancing binary search tree using algorithm define by
 * Adelson-Velskii and Landis.
 * @param <E> Type contained in the tree.
 */
public class AVLTree<E extends Comparable<E>> extends BinarySearchTreeWithRotate<E> {
    // Data Fields
    /** Flag to indicate that height of tree has increased. */
    private boolean increase;
}

5.4.2. Insertion

To insert a new node containing \(X\) into the tree \(T\):

5.4.2.1. Insert

We will optimize the code of the AVl tree, but we will try to make it readable.

We will consider the following functions:

• The add function

• The rebalanceLeft function

• The rebalanceRight function

The add one is identical to the one in the binary tree search, except for the private one in which we need to launch the rebalanceLeft or rebalanceRight after the insertion.

    /**
     * Recursive add method. Insert the given item into the tree.
     * @param localRoot The local root of the subtree
     * @param item The item to insert
     * @return The new local root of the subtree with the item inserted
     */
    private AVLNode<E> add(AVLNode<E> localRoot, E item){
        if (localRoot == null){
            addReturn= true;
            increase = true;
            return new AVLNode<E>(item);
        }
        if (item.compareTo(localRoot.data) == 0){
            // Item is already in the tree.
            increase = false;
            addReturn = false;
            return localRoot;
        } else if (item.compareTo(localRoot.data) < 0) {
            // item < data
            localRoot.left = add((AVLNode<E>) localRoot.left, item);
            if (increase){
                decrementBalance(localRoot);
                if (localRoot.balance < AVLNode.LEFT_HEAVY) {
                    increase = false;
                    return rebalanceLeft(localRoot);
                }
            }
        } else if (item.compareTo(localRoot.data) > 0) {
            // item > data
            localRoot.right = add((AVLNode<E>) localRoot.right, item);
            if (increase){
                incrementBalance(localRoot);
                if (localRoot.balance > AVLNode.RIGHT_HEAVY) {
                    increase = false;
                    return rebalanceRight(localRoot);
                }
            }
        }
        return localRoot;
    }

This way the balancing will be done at each level, if necessary.

Note that we are using two functions decrementBalance(localRoot); and incrementBalance(localRoot);.

Indeed we need to update the balance of each node on the path to the root or until a rebalance is done.

    /**
     * Decrement the balance of the given node
     * @param node The node to decrement the balance of
     */
    private void decrementBalance(AVLNode<E> node) {
        // Decrement the balance.
        node.balance--;
        if (node.balance == AVLNode.BALANCED) {
            /* If now balanced, overall height has not increased. */
            increase = false;
        }
    }

    /**
     * Increment the balance of the given node
     * @param node The node to increment the balance of
     */
    private void incrementBalance(AVLNode<E> node){
        node.balance++;
        if(node.balance == AVLNode.BALANCED){
            //If now balanced, overall height has not increased
            increase = false;
        }
    }

5.4.2.2. Balance

We need to consider different cases:

• The difference between the left subtree and the right subtree is greater than 1.

  • Check if the depth is greater on the exterior (left-left)

    • Simple rotation on the left.

  • Otherwise, double rotation on the left.

• Otherwise, check the difference between the right subtree and the left subtree is greater than 1.

  • Check if the depth is greater on the exterior (right-right).

    • Simple rotation on the right.

  • Otherwise double rotation on the right.

We will use 2 private methods for the rotations:

    /**
     * Method to rebalance left.
     * @param localRoot Root of the AVL subtree that needs balancing.
     * @return A new localRoot
     */
    private AVLNode<E> rebalanceLeft(AVLNode<E> localRoot){
    }
    /**
     * Method to rebalance right.
     * @param localRoot Root of the AVL subtree that needs balancing.
     * @return A new localRoot
     */
    private AVLNode<E> rebalanceRight(AVLNode<E> localRoot){
    }

The first one rebalanceLeft can be written as:

    /**
     * Method to rebalance left.
     * @param localRoot Root of the AVL subtree that needs balancing.
     * @return A new localRoot
     */
    private AVLNode<E> rebalanceLeft(AVLNode<E> localRoot){
        // Obtain reference to left child.
        AVLNode<E> leftChild = (AVLNode<E>) localRoot.left;
        // Check if left-right heavy
        if (leftChild.balance > AVLNode.BALANCED){
            // Obtain reference to left-right child
            AVLNode<E> leftRightChild = (AVLNode<E>) leftChild.right;
            if(leftRightChild.balance < AVLNode.BALANCED){
                leftChild.balance = AVLNode.BALANCED;
                leftRightChild.balance = AVLNode.BALANCED;
                localRoot.balance = AVLNode.RIGHT_HEAVY;
            } else if (leftRightChild.balance > AVLNode.BALANCED){
                leftChild.balance = AVLNode.LEFT_HEAVY;
                leftRightChild.balance = AVLNode.BALANCED;
                localRoot.balance = AVLNode.BALANCED;
            } else {
                //Left-Right balanced case
                leftChild.balance = AVLNode.BALANCED;
                localRoot.balance = AVLNode.BALANCED;
            }
            localRoot.left = rotateLeft(leftChild);
        }
        else{
            // Left-left case
            leftChild.balance = AVLNode.BALANCED;
            localRoot.balance = AVLNode.BALANCED;
        }
        // Now rotate on the right.
        return (AVLNode<E>) rotateRight(localRoot);
    }
    /**
     * Method to rebalance right.
     * @param localRoot Root of the AVL subtree that needs balancing.
     * @return A new localRoot
     */
    private AVLNode<E> rebalanceRight(AVLNode<E> localRoot){
    }

Activity

• Implement the rebalanceRight method.

    /**
     * Method to rebalance right.
     * @param localRoot Root of the AVL subtree that needs balancing.
     * @return A new localRoot
     */
    private AVLNode<E> rebalanceRight(AVLNode<E> localRoot){
    }

Rotations

As you can see we need to define the two rotation functions:

• rotateLeft

• rotateRight

Starting with rotateLeft.

The following figure illustrates the idea.

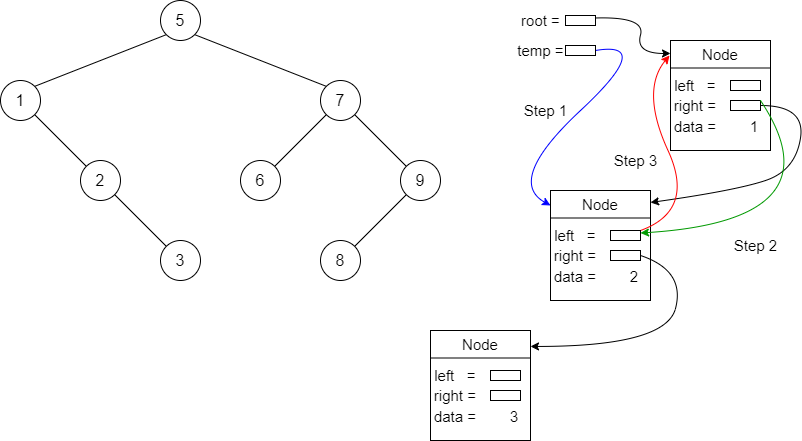
Which is very simple to implement:

    /**
     * Method to perform a left rotation.
     * @post root.left is the root of a binary search tree,
     *       root.left.left is raised one level,
     *       root.left.right does not change levels,
     *       root.right is lowered one level,
     *       the new root is returned.
     * @param root is the root of a binary search tree
     * @return The new root of the rotated tree
     */
    protected Node<E> rotateLeft(Node<E> root) {
        Node<E> temp = root.right;
        root.right = temp.left;
        temp.left = root;
        return temp;
    }

Activity

• Implement rotateRight

• It’s the symmetric function:

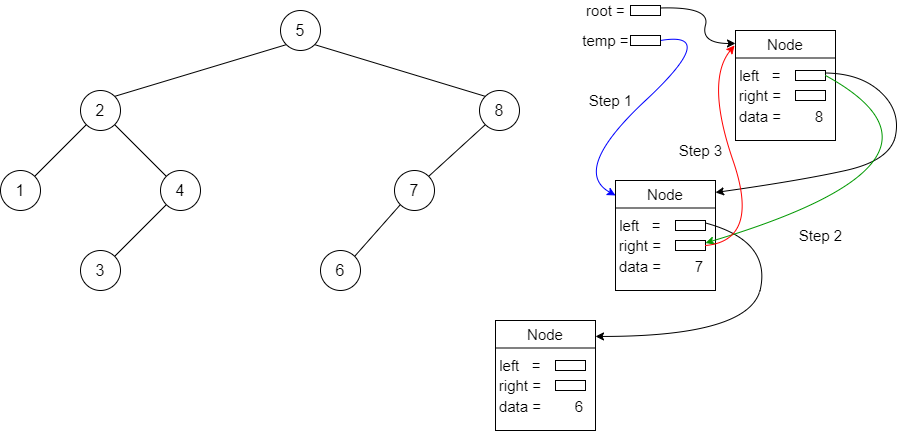
5.4.3. Deletion

We didn’t talk about removing a node.

Again it is the same as for the binary tree search, but we need to balance the tree after each deletion.

5.4.4. Other operations

Everything else is exactly the same as in the binary tree search ADT.

And it should not surprise you.

The AVL Tree is just a self-balancing BST, nothing more, nothing less.