7. B-Trees

In this topic we will discuss nonbinary trees.

We will start with the 2-3-tree that is a simpler version of the general B-tree.

7.1. 2-3-tree

A 2-3-tree is a tree that has 2 or 3 children for each node.

These nodes are called 2-nodes and 3-nodes:

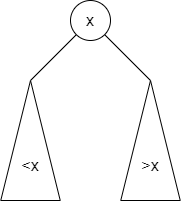
• 2-nodes:

  • There are similar to the binary tree search nodes.

  • They contain one attribute and references to two children.

  

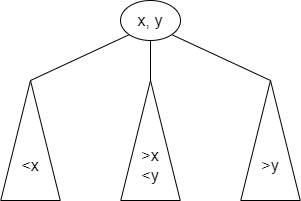
• 3-nodes:

  • There are different as they contain two attributes ordered so the first one is less than the second. It also references three children.

  • The first child containing a value less than the first attribute.

  • The second has a value between the first and second attributes.

  • And the last has a value greater than the second attribute.

  

Important

The main property is that all the leaves are at the lowest level of the tree.

This is how this type of tree maintain the balance!

Activity

• Consider the following tree.

• Ensure that the property of a 2-3-tree is respected.

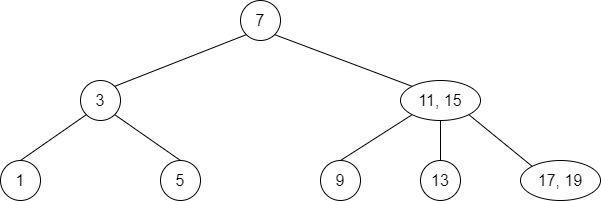
• Think of a search strategy to find an element in a 2-3-tree.

7.1.1. Operations

2-3-trees are different from the regular binary search trees that we covered until now, so we need to redefine all the operations:

• Search

• Insert

• Remove

7.1.2. Search

The search algorithm is more similar to the binary search tree that we could expect.

The pseudocode of the search can be written as follow:

if  the local root is null:
    return null
else if 2-node:
    if item = data1:
        return data1
    else if item < data1:
        recursively search the left subtree
    else:
        recursively search the right subtree
else:
    if item = data1:
        return data1
    else if item = data2:
        return data2
    else if item < data1:
        recursively search the left subtree
    else if item < data2:
        recursively search the middle subtree
    else:
        recursively search the right subtree

Activity

• Apply the previous algorithm to find if 13 is in the following tree.

7.1.3. Insertion

When we insert a new item, we need to make sure that the tree stay balanced. The main difference with 2-3-trees is that the balance is down by building the tree from the bottom up and not the top down.

The idea:

• Start by finding where to insert the new item by using the search method defined previously.

• Insert the new item inside a node and not attached to a node.

Contrary to a regular binary search tree, we can be in three cases:

• Case 1: Inserting into a 2-node leaf.

• Case 2: Inserting into a 3-node leaf with 2-node parent.

• Case 3: Inserting into a 3-node leaf with 3-node parent.

7.1.3.1. Case 1: 2-node leaf

This is the easiest case. If the leaf is a 2-node then there is enough space to insert an element inside it, thus creating a 3-node.

Example

• Consider the tree on the left.

• If we insert 15 inside it, then we find a 2-node, 11, that can accept a new item inside it.

7.1.3.2. Case 2: 3-node leaf with 2-node parent

This case happens when the node we want to insert the item is already a 3-node and the parent is a 2-node parent.

As 3-node cannot store three values, the strategy is to transform the parent node (which is a 2-node) to a 3-node by inserting the middle value in the parent directly.

However, if we do that the smallest item is not at the correct position in the tree, so we need to create a middle node for the parent containing the smallest value.

Example

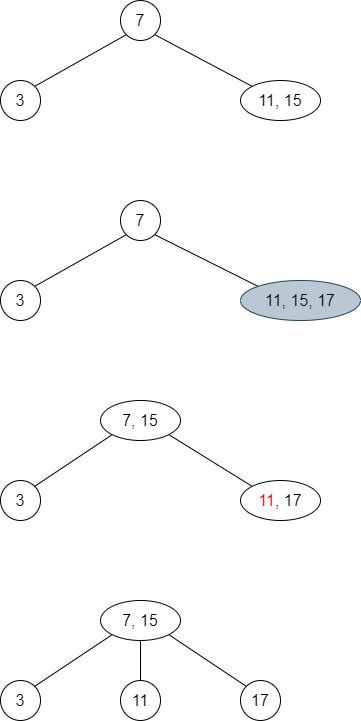
• Consider the tree in the previous example.

• If we insert 17 inside it, then we find a 3-node 11, 15.

• This node cannot contain three values, so we take the middle value 15 and insert it in the parent 7.

• Now, 11 is misplaced, so create a middle node of 7, 15 with 11.

• The following trees shows the insertion step by step:

Activity

• Insert 5, 10 and 20.

7.1.3.3. Case 3: 3-node leaf with 3-node parent

This case happens when the node we want to insert the item is already a 3-node and the parent is also a 3-node parent.

As 3-node cannot store three values, we need to propagate up the middle value of the virtual node, as seen before.

However, the parent node is also a 3-node, so we apply the same strategy and propagate up again.

Example

• Consider the following example.

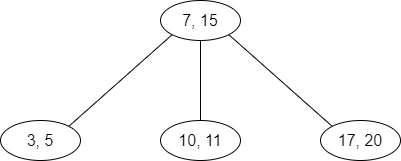
• Now, if we insert 13, then a 3-node get a third value.

• To solve that we propagate up the middle value (11) of the node.

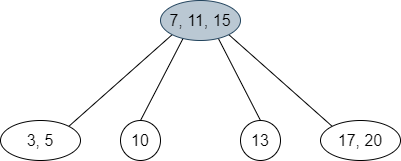
• The parent was a 3-node, so we repeat the strategy and propagate up the middle value, creating a new root with two children.

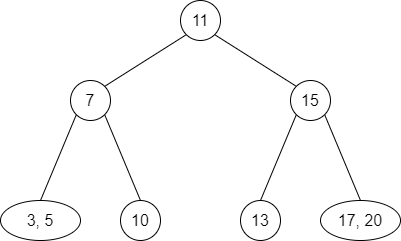
• We can see that the properties of a 2-3-tree are followed.

The general pseudocode for insertion can be written as follow:

if root is null:
    Create a 2-node with the new item
else if item in root:
    return False
else if root is leaf:
    if root is 2-node:
        expand 2-node to 3 and insert item
    else:
        Create two 2-nodes and propagate up the new parent and the right child.
else:
    if item < smaller item in local root:
        insert left
    else if local root is 2-node:
        insert right
    else if item < larger item in local root:
        insert middle
    else:
        insert right
    if new parent was propagated up:
        if new parent will be the tree root:
            Create 2-node with new parent
            Left child is old parent
            Right child is the propagated up child
            The 2-node becomes the new parent
        else:
            Insert new parent at local root
return True

7.1.4. Analysis

Before going further we need to discuss the advantages of a 2-3-tree.

Activity

• Discuss the advantages of a 2-3-tree against AVL trees or Red-Black Trees.

The number of items that can contain a 2-3-tree of height \(h\) is between \(2^h - 1\) and \(3^h - 1\).

Meaning that the height of 2-3-tree is between \(\log_3 n\) and \(\log_2 n\).

Thus the search time is \(O(\log n)\).

7.1.5. Deleting

Deleting an item is very similar to inserting an item.

The idea:

• Find the item to remove.

• If the item is a leaf -> remove it

• Otherwise we swap it with its inorder predecessor in a leaf node and delete it in the leaf node.

• If removing an item empty a leaf.

  • Items from the sibling and parent can be redistributed into that leaf.

  • Or the leaf can be merged with its parent and sibling.

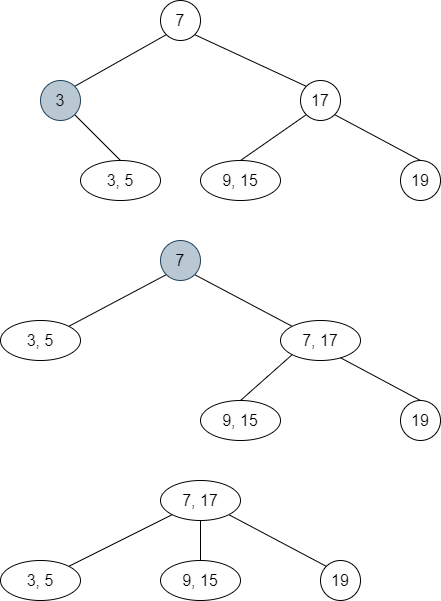
Example

• Consider the following tree:

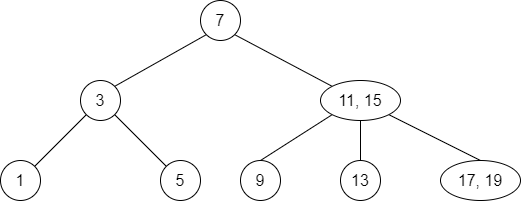
• If we remove 13, the node becomes empty and 15 in the parent node will not have left child.

• We can merge 15 with the right child creating the virtual node 15, 17, 19.

• Then, we propagate up 17 similarly to the insertion strategy.

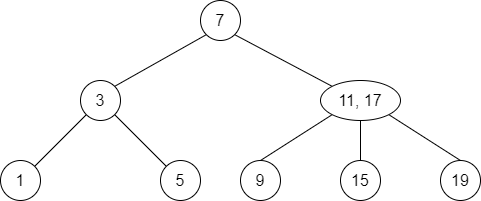
• Now we remove 11.

• As it’s not a leaf we replace it with its predecessor 9.

• Now the leaf is empty, so we merge its right child 15.

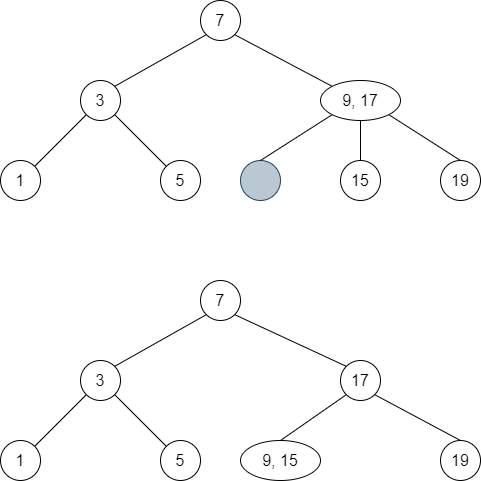
• Finally, we remove 1.

• First we merge 3 with its right child 5; it empties 3.

• So the process repeat with 7 and its right child 17.

• It becomes the root node.

7.2. B-Trees

The 2-3-tree is inspired the B-trees which allow up to \(n\) children per node, where \(n\) can be a very large number.

Originally, B-trees are designed to build indexes to very large databases stored on a hard disk.

In the B-tree, the maximum number of children is the order of the B-tree.

The general properties for B-trees are:

• Other than the root, each node has between order/2 and order children.

• The number of items in a node is number_of_children - 1.

• The data items in each node are ordered.

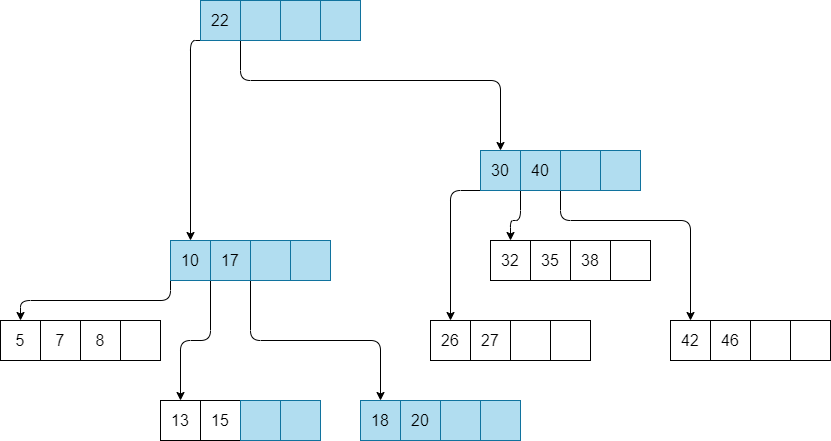
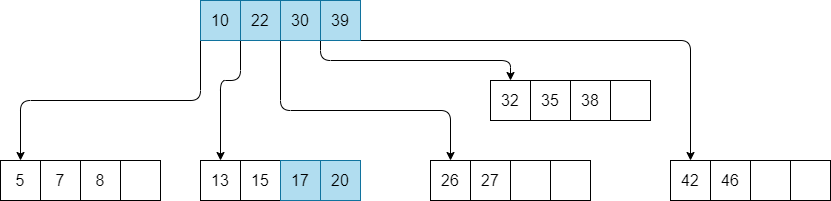
Below is an example of a B-tree:

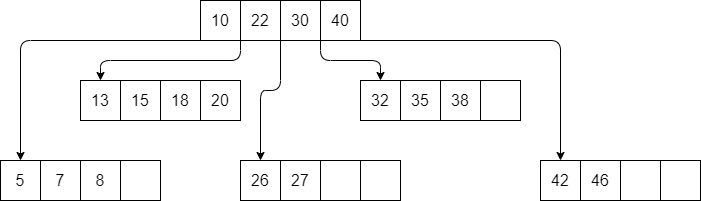
Actvity

• What is the order of the B-Tree?

7.2.1. Insertion

The insertion is similar to the 2-3-trees:

• The new item is always inserted in a leaf.

• If the leaf is not full, we are done.

• Otherwise, if the leaf is full it is split into two nodes with the middle node propagated up.

• If the root is being split, then the middle item becomes the new root.

Example

• If we take the previous B-tree and we insert 17 we obtain the following new tree.

The pseudocode for insertion is:

if the root is null
    Create a new Node that contains item
else search item in local root:
    if item in local root:
        return False
    else:
        if local root is leaf:
            if local root is null:
                insert new item
                return null as the newChild and True to indicate successful insertion
            else:
                split local root
                return newParent and newChild and True to indicate successful insertion
        else:
            recursively call insert
    if newChild is not null:
        if local root not null
            insert newParent and newChild in local root
            return null as the newChild and True to indicate successful insertion
        else:
            split local root
            return newParent and newChild and True to indicate successful insertion
    else:
        return success/fail indicator for the insertion

Important

The code and pseudocode is the hardest covered in class. You’re not expected to be able to implement it, but you should understand how it works.

7.2.2. Deletion

Removing an item in a B-tree is a generalization of a removing an item from a 2-3-tree.

We can distinguish two main cases:

• The item is in a leaf.

  • Then we just remove it.

• If the item is in an interior node:

  • It can’t be deleted otherwise it will damage the B-tree properties.

  • The item must be replaced by its inorder predecessor.

We also need to consider the case in which deleting an item in a leaf results in a leaf being half full.

• In this case, items from a sibling node and parent are redistributed into that leaf.

• However if the sibling is itself exactly half full, the leaf, its parent item and siblings are merged into a single node.

Example

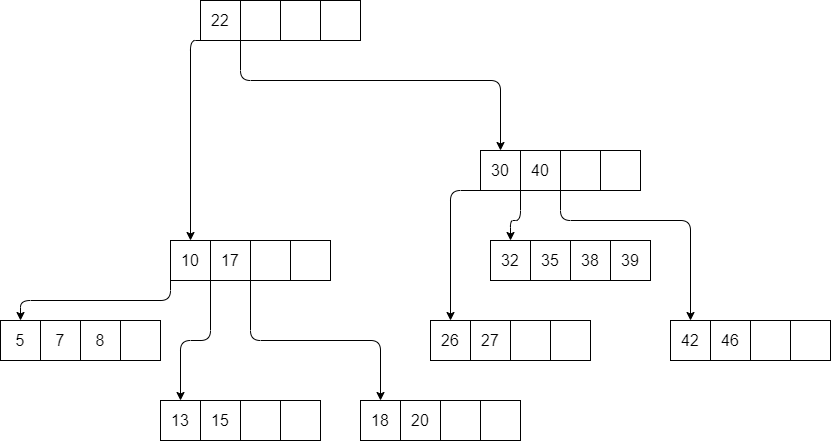
• Consider the following B-tree.

• If we remove 40, we are in the second case man case.

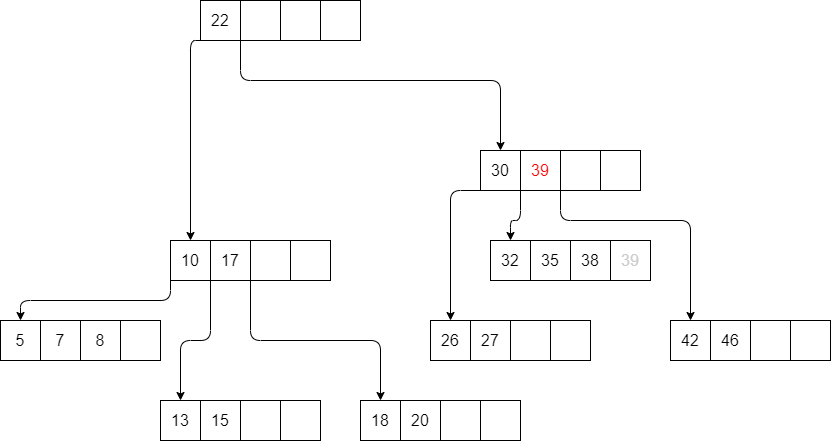
• We replace its inorder predecessor.

• In this case 39.

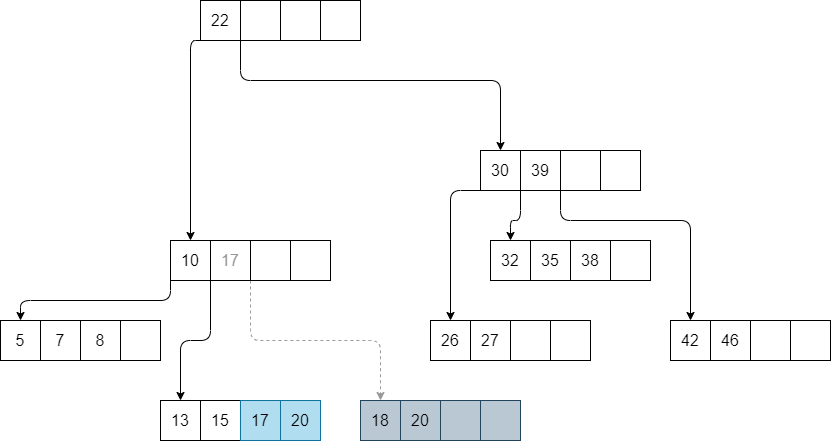
• Now, we want to remove 18.

• If we remove it, the leaf will have less than half full.

• Because the sibling is exactly half full, we can merge the parent item and the leaf together.

• Once done, the parent node containing 10 is less than half full.

• The sibling is also exactly half full, so we repeat the procedure.

• The B-tree doesn’t break any B-tree properties so we can stop.