11. Graph

• Graphs are a special type of data structure.

• They are used to solve many problems, such as the shortest path problem.

• However, if the implementation is not done carefully it can be too slow to use.

11.1. What is a graph?

• We will start by giving a definition of a graph.

Definition: Graph

• A graph \(G = (V,E)\) consists of a set of vertices \(V\) and a set of edges \(E\).

• Each edge is a pair \((v, w)\), where \(v,w\in V\).

• Edges are sometimes referred as arcs and vertices as nodes.

11.1.1. Directed Graphs

Definition: Directed Graph

• When the edges (or arcs) \((v,w)\) are ordered the graph is directed.

• Vertex \(w\) is adjacent to \(v\) if and only if \((v,w)\in E\).

• Directed graphs are also referred as digraphs.

• The following figure represents a digraph:

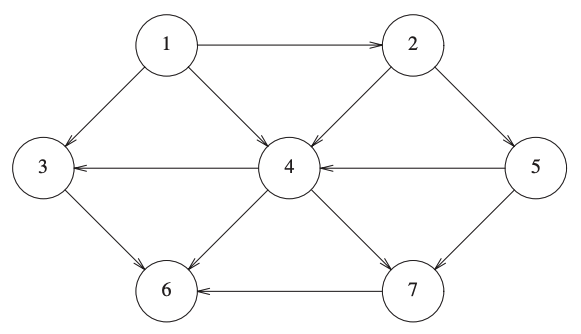
Activity

• Write all the pairs \((v,w) \in E\) of the previous graph.

11.1.2. Undirected Graphs

• If there are directed graphs, there are undirected graphs!

Definition: Undirected Graph

• In an undirected graph with edges \((v,w)\in E\), there is an edge \((w,v)\in E\).

• \(w\) is adjacent to \(v\) and \(v\) is adjacent to \(w\).

Activity

• Take the previous graph and transform it to an undirected graph.

• Draw the undirected graph that contains the following edges:

  • \(E = \{(a,b), (b,a), (a,c), (c,a), (b,c), (c,b)\}\)

11.2. Representing graph in memory

• Obviously, we cannot represent a graph like this in memory.

• We could be as close as possible to the math representation:

  • Storing a list of nodes

  • And storing the list of arcs.

Activity

• What do you think about this representation?

• Do you have a better representation?

• There are two ways to represent a graph in memory:

  • Adjacency matrix

  • Adjacency list

11.2.1. Adjacency Matrix

• The easiest way to represent is with a 2D matrix.

• This is called an adjacency matrix.

The idea:

• Consider a matrix \(M\).

• For each \((u,v) \in E\):

  • We set \(M[u][v]\) to 1.

  • Otherwise to 0.

Example

• If we take the previous graph.

• We can create the following adjacency matrix.

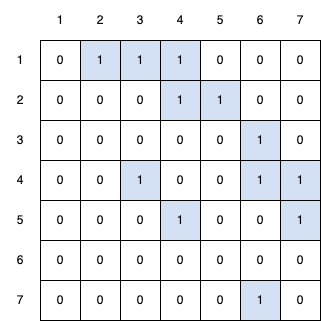
• It is very easy to use adjacency matrix and very fast.

• However, the space requirement is \(O(|V|^2)\).

  • It is a lot if the graph has an important number of nodes, but few arcs.

  • It is appropriate if the graph is dense \(|E| = O(|V|^2)\).

Activity

• Why using a matrix for dense graphs is not a problem?

• In most problems, graphs are not dense.

Example

• Consider a street map of a city.

  • Assume a Manhattan-like orientation.

  • Any intersection is attached to roughly 4 streets.

• So, if the graph is directed with two-way streets.

  • The number of edges is \(|E| \approx 4|V|\)

• If there are 3 000 intersection.

  • The number of vertices is 3 000.

  • And the number of edges is 12 000.

• It requires an array of size 9 000 000.

• A graph that is not dense is called sparse.

• We need another way to represent sparse graph.

11.2.2. Adjacency List

• Adjacency list is a better solution when the graph is sparse.

• For each vertex, we keep a list of all adjacent vertices.

Example

• If we take the previous graph.

• We can create the following adjacency list.

  • The space requirement is \(O(|E|+|V|)\).

  • It is linear in the size of the graph.

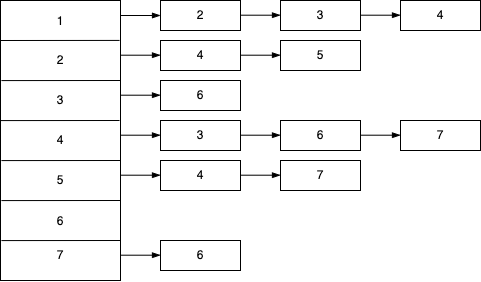
Activity

• Why are we not using adjacency lists for dense graphs?

11.2.3. Weighted edges

• Consider a problem in which you need to represent the streets and intersections in a city.

• You would like to store the distance of each street.

• A graph allows us to add weights on edges.

• The changes to the previous representation are small:

  • Adjacency matrix: Instead of 0 and 1, we have the weight of the edge if it exists. If not \(- \infty\) or \(+ \infty\).

  • Adjacency list: Add a new element in the list.

Activity

• Draw the directed graph that contains the following edges:

  • \(E = \{(a,b,2), (b,a,4), (a,c,3), (c,a,1), (b,c,10)\}\)

• Give the adjacency matrix and adjacency lists representation.

11.3. Implementation

• Java does not provide an implementation of the Graph ADT.

• We will write our own!

• We want our ADT to be able to do the following:

  • Create a graph with the specified number of vertices.

  • Iterate through all the vertices in the graph.

  • Iterate through the vertices that are adjacent to a specified vertex.

  • Determine whether an edge exists between two vertices.

  • Determine the weight of an edge between two vertices.

  • Insert an edge into the graph.

11.3.1. The Graph interface

We want to define a Graph interface that will not depend of the memory representation.

It will have the following methods:

• int getNumV(): Returns the number of vertices in the graph

• int isDirected(): Return if the graph is directed

• Iterator<Edge> edgeIterator(int source): Returns an iterator to the edges that originate from a given vertex

• Edge getEdge(int source, int dest): Gets the edge between two vertices

• void insert(Edge e): Insert a new edge into graph

• boolean isEdge(int source, int dest): Determines whether an edge exists from source to dest

• default void loadEdgesFromFile(Scanner scan): A default method that loads the edges from a file associated with scan

package graph;

import java.util.*;

/** Interface to specify a Graph ADT.
 * A graph is a set of vertices and a set of edges.
 * Vertices are represented by integers from 0 to n − 1.
 * Edges are ordered pairs of vertices.
 * Each implementation of the Graph interface should
 * provide a constructor that specifies the number of
 * vertices and whether the graph is directed.
 */
public interface Graph {

    // Accessor Methods
    /** Return the number of vertices.
     @return The number of vertices
     */
    int getNumV();

    /** Determine whether this is a directed graph.
     @return true if this is a directed graph
     */
    boolean isDirected();

    /** Insert a new edge into the graph.
     @param edge The new edge
     */
    void insert(Edge edge);

    /** Determine whether an edge exists.
     @param source The source vertex
     @param dest The destination vertex
     @return true if there is an edge from source to dest
     */
    boolean isEdge(int source, int dest);

    /** Get the edge between two vertices.
     @param source The source vertex
     @param dest The destination vertex
     @return The edge between these two vertices or null if there is no edge
     */
    Edge getEdge(int source, int dest);

    /** Return an iterator to the edges connected to a given vertex.
     @param source The source vertex
     @return An Iterator<Edge> to the vertices connected to source
     */
    Iterator<Edge> edgeIterator(int source);

    /** Read source and destination vertices and weight (optional) for each edge from a file
     @param scan The Scanner associated with the file
     */
    default void loadEdgesFromFile(Scanner scan) {
        String line;
        while (scan.hasNextLine()) {
            line = scan.nextLine();
            if (!line.isBlank()) {
                String[] tokens = line.split("\\s+");
                int source = Integer.parseInt(tokens[0]);
                int dest = Integer.parseInt(tokens[1]);
                double weight = 1.0;
                if (tokens.length == 3) {
                    weight = Double.parseDouble(tokens[2]);
                }
                insert(new Edge(source, dest, weight));
            }
        }
    }
}

11.3.2. Edge Representation

The nodes will be represented by integers, but we need a class to represent the edge.

The class is simple, it contains three attributes:

• A source node

• A destination node

• A weight, \(1\) by default.

/**
 * An Edge represents a relationship between two
 * vertices.
 */
public class Edge {
    // Data Fields
    /** The source vertex */
    private final int source;
    /** The destination vertex */
    private final int dest;
    /** The weight */
    private final double weight;

    // Constructor
    /** Construct an Edge with a source of from
     * and a destination of to. Set the weight to 1.0.
     * @param source - The source vertex
     * @param dest - The destination vertex
     */
    public Edge(int source, int dest) {
    }
    /** Construct a weighted edge with a source
     * of from and a destination of to. Set the
     * weight to w.
     * @param source - The source vertex
     * @param dest - The destination vertex
     * @param w - The weight
     */
    public Edge(int source, int dest, double w) {
    }
    // Methods
    /** Get the source
     * @return The value of source
     */
    public int getSource() {
    }
    /** Get the destination
     * @return The value of dest
     */
    public int getDest() {
    }
    /** Get the weight
     * @return the value of weight
     */
    public double getWeight() {
    }
    /** Return a String representation of the edge
     * @return A String representation of the edge
     */
    @Override
    public String toString() {
    }
    /** Return true if two edges are equal. Edges
     * are equal if the source and destination
     * are equal. Weight is not considered.
     * @param obj The object to compare to
     * @return true if the edges have the same source
     * and destination
     */
    @Override
    public boolean equals(Object obj) {
        if (obj instanceof Edge) {
            Edge edge = (Edge) obj;
            return (source == edge.source && dest == edge.dest);
        } else {
            return false;
        }
    }
    /** Return a hash code for an edge. The hash
     * code is the source shifted left 16 bits
     * exclusive or with the dest
     * @return a hash code for an edge
     */
    @Override
    public int hashCode() {
        return (source << 16) ^ dest;
    }

11.3.3. Adjacency List Representation

We will create a class to represent a graph using a linked list.

This class ListGraph will implement the interface Graph and contains three attributes.

import java.util.*;

/** A ListGraph implements the Graph interface using an
 array of lists to represent the edges.
 */
public class ListGraph implements Graph {

    // Data Fields
    /** The number of vertices */
    private final int numV;
    /** An indicator of whether the graph is directed (true) or not (false)
     */
    private final boolean directed;
    /** An array of Lists to contain the edges that
     originate with each vertex.
     */
    private LinkedList<Edge>[] edges;
}

The constructor only takes the number of nodes and if the graph is directed as parameters.

    /** Construct a graph with the specified number of vertices and directionality.
     @param numV The number of vertices
     @param directed The directionality flag
     */
    public ListGraph(int numV, boolean directed) {
        this.numV = numV;
        this.directed = directed;
        edges = new LinkedList[numV];
        for (int i = 0; i < numV; i++) {
            edges[i] = new LinkedList<Edge>();
        }
    }

Activity

Implement the following methods of the class.

    /**
     * Insert a new edge into the graph.
     *
     * @param edge The new edge
     */
    @Override
    public void insert(Edge edge) {
    }
    /**
     * Get the edge between two vertices.
     *
     * @param source The source vertex
     * @param dest   The destination vertex
     * @return The edge between these two vertices
     * or null if there is no edge
     */
    @Override
    public Edge getEdge(int source, int dest) {
    }

11.4. More Definitions

• Graphs are used in a lot of algorithms.

• To use them in these algorithms, we require some last definitions.

Definition: Path

• In a graph, a path is a sequence of vertices \(v_1, v_2 \dots, v_N\) such that \((v_i, v_{i+1})\in E\) for \(1 \leq i < N\).

• The length of the path is the number of edges on the path (\(N-1\)).

Definition: Cycle

• In a cycle in a directed graph is a path of length at least 1 such that \(v_1 = v_N\).

• In undirected graph the edges need to be distinct.

• If a directed graph does not have a cycle, it is called a acyclic graph.

Activity

• Consider the graph given in the first example.

• Give an example of a path.

• Give a example of a cycle.