12. Graph Algorithms

Now we have the tools to see some graph algorithms.

12.1. Topological Sort

• A topological sort is an ordering of nodes in a directed acyclic graph.

• If there is a path from \(v_i\) to \(v_j\).

• Then \(v_j\) appears after \(v_i\) in the ordering.

Example

• Following an acyclic graph.

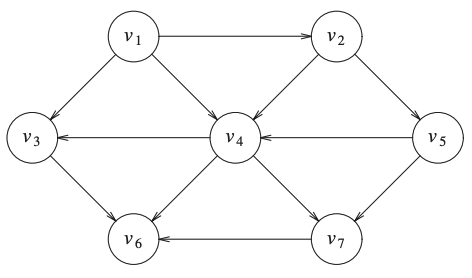
• An example of a topological ordering: \(v_1, v_2, v_5, v_4, v_7, v_3, v_6\).

Activity

• Give another topological ordering.

12.1.1. A Simple Algorithm

• We define the indegree of a node \(v\), as the number of edges \((u,v)\).

• A simple algorithm to find topological ordering is:

  • Find any vertex with an indegree of 0.

  • Remove it along with its edges.

  • Apply the strategy with another vertex.

• We obtain the following pseudocode:

void topsort()
{
    for (int counter = 0; counter < NUM_VERTICES; counter++){
        Vertex v = findNewVertexOfIndegreeZero();
        if (v == NOT_A_VERTEX){
            throw CycleFoundException();
        }
        v.topNum = counter;
        for each Vertex w adjacent to v{
            w.indegree--;
        }
    }
}

• Where findNewVertexOfIndegreeZero() scans the array of vertices looking for a vertex with indegree 0.

• If it returns NOT_A_VERTEX it indicates that the graph has a cycle.

• The complexity of this algorithm \(O(|V|^2)\).

12.1.2. A Second Algorithm

• The graph could be parsed, so checking each vertex could be a waste of time.

• A second way to make a topological sort is to place every vertex of indegree 0 in a queue.

• While the queue is not empty we remove one vertex.

• All the adjacent vertices have their indegree decremented.

Following a pseudo-code of the algorithm:

void topsort()
{
    Queue<Vertex> q;
    int counter = 0;

    q.makeEmpty( );
    for each Vertex v
        if( v.indegree == 0 )
            q.enqueue( v );

    while( !q.isEmpty( ) )
    {
        Vertex v = q.dequeue( );
        v.topNum = ++counter; // Assign next number
        for each Vertex w adjacent to v
            if( --w.indegree == 0 )
                q.enqueue( w );
    }

    if( counter != NUM_VERTICES )
        throw CycleFoundException();
}

• The running time of this algorithm is \(O(|E|+|V|)\).

Activity

• Can you explain the running time?

• Apply this algorithm to the previous graph.

12.2. Shortest-Path Algorithms

• There are different shortest-path algorithms.

• But, they have common properties:

  • The input is a weighted graph.

  • The weight for each edge \((v_i, v_j)\) is a cost \(c_{i,j}\) to traverse the edge.

  • The cost of a path \(v_1v_2\dots v_N\) is \(\sum_{i=1}^{N-1}c_{i,i+1}\).

Activity

• What would be the cost of the path in an unweighted graph?

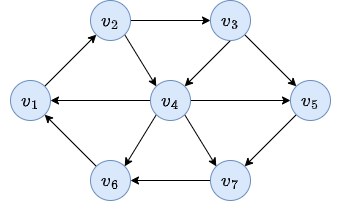
• Consider the previous graph:

  • What is the cost of the path \(v_1, v_2, v_5, v_7\).

  • Do you have a shorter path from \(v_1\) to \(v_7\)?

12.2.1. Breadth-First Search

• Finding the shortest path in an unweighted graph is considering a weighted graph where all the edges have a cost of 1.

• It is minimizing the number of edges in the path.

• We will introduce a single source shortest-path algorithm for unweighted graph \(G = (V, E)\).

  • Single source means that we calculate the shortest path from a specific node \(s \in V\) to any other nodes \(v_k \in V\).

A very simple algorithm is breadth-first search.

The idea is to process nodes in layers.

Example

• Consider the previous unweighted directed graph.

• We want to apply breadth first to find the shortest path from \(v_1\) to \(v_6\).

• We obtain the following steps:

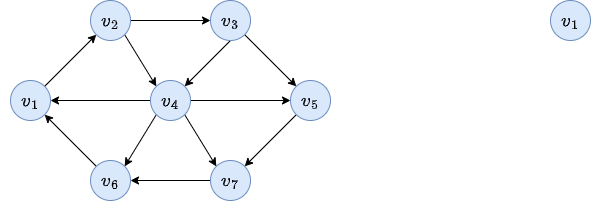
We start with the first node \(v_1\).

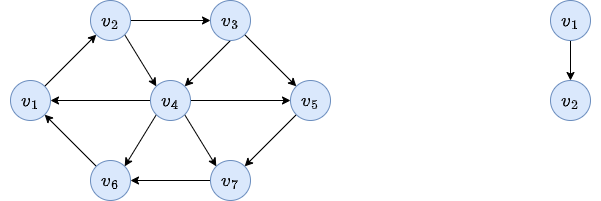
We check each arc leaving \(v_2\).

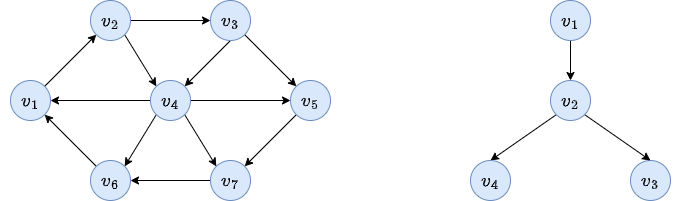
We check each arc leaving \(v_4\).

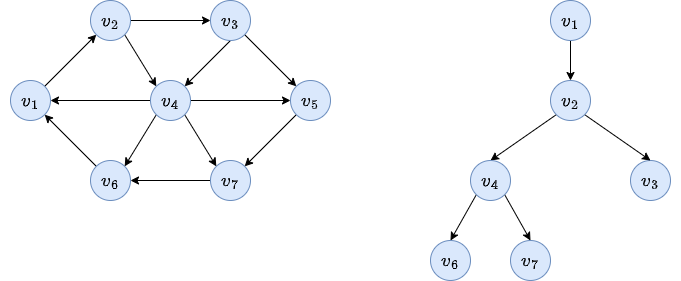
Finally, the arcs leaving \(v_3\).

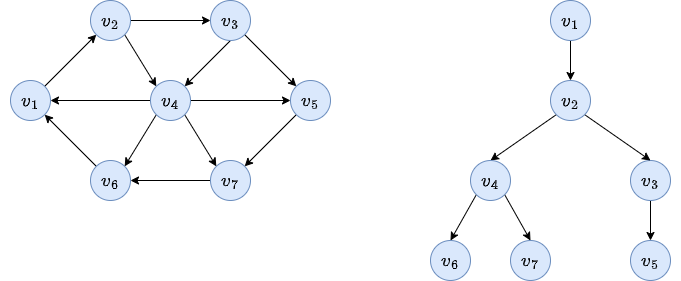
Activity

• Apply the algorithm to find the shortest path from \(v_4\) to \(v_1\).

12.2.1.1. Implementation

• First we create a table that will keep track of the algorithm progress.

• The table will keep track for each node it was visited or marked.

The pseudo-code is given below:

function BFS(Graph, source):

    Create a queue Q.
    Q.insert(s).

    while Q not empty:
        u = Q.pop()
        visit(u)
        for all v adjacent to u:
            if v not marked or visited:
                Mark v
                Q.insert(v)

• The complexity of this algorithm is \(O(|V|^2)\).

Activity

• Is the algorithm efficient?

• If not, how would you improve it?