Topic 10 - Markov Decision Process

  • Until now we have seen how a robot move or locate itself.

  • It is important now to cover how a robot can plan its mission.

  • We will now cover probabilistic algorithms.

Motivation

We can take a few examples:

  1. A robotic manipulator grasp and assembles parts arriving in random configuration on a conveyor belt.

  • The parts that arrive are unknown.

  • The optimal strategy requires to know the future parts.

  1. A vehicle to move from point A to point B in Toronto.

  • Shall it take the shortest path through downtown, but losing the GPS.

  • Or shall it takes the longest path, but keeping the GPS.

  1. Robots need to map an area collectively.

  • Should they seek each other?

  • Or should they cover more unknown area alone?

In robotics we need to consider two types of uncertainties:

  • Uncertainty of the actions.

  • Uncertainty on the measurement.

Activity

  • How would you handle these two uncertainties?

Markov Decision Process

  • We will star by tackling the problem of the uncertainty on the actions.

  • Markov Decision Process or called MDP is a mathematical framework that allows us to consider stochastic environment.

The Idea

  • MDPs can be represented graphically as follows:

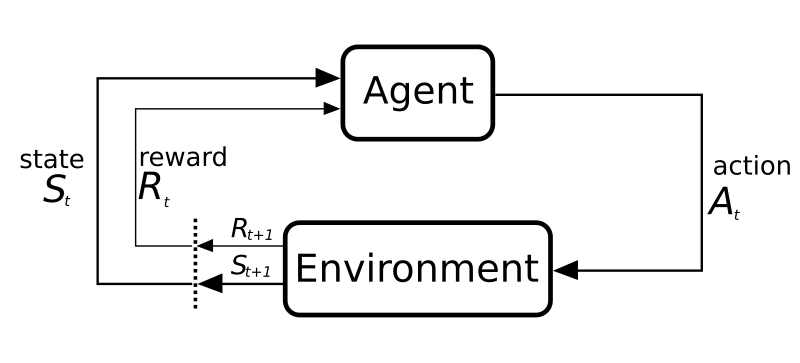
_images/mdp.png

  • We have an agent, in our case a robot.

  • These agents evolve in an environment.

  • The agent can interact with this environment with different actions.

  • When the agent uses an action it changes the state of the environment and it gives it a reward.

Activity

  • Consider a robot that needs to navigate in a maze.

  • Try to answer the following questions:

    • What would be the environment?

    • What would be the actions?

    • What would be the state?

Formally

  • We need to define MDPs formally.

Definition

A MDP is defined with a tuple \((S,A,T,R)\):

  • \(S\) is the state space that contains the set of states \(s\in S\).

  • \(A\) is the action space that contains the set of actions \(a\in A\).

  • \(T: S\times A\times S\) is the transition function that defines the probability \(p(s_{t+1}=s'|s_{t}=s,a_{t})\).

  • \(R: S\times A \rightarrow \mathbb{R}\) is the reward function that defines \(r(s,a)\).

Activity

  • Remember the problem of detecting Alan in the hallway?

    • Alan can only move forward.

    • At each time step, Alan can ever overshoot by 1 cell with a probability of 10%.

    • Alan can ever undershoot by 1 cell with a probability of 10%.

  • Now we want to model Alan moving in the hallway as an MDP:

    • Define the state space.

    • Define the action space.

    • Define the transition function.

Solving a MDP

  • The strategy in an MDP is called a policy \(\pi: S \rightarrow A\).

    • It’s a function that gives for each state \(s\in S\) the action \(a\in A\).

    • When a policy is followed we obtain a trajectory \(G\).

    • Which is a sequence of rewards:

\[G_t = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \dots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1}\]

where \(\gamma\) is a discount rate \(0 \leq \gamma \leq 1\).

  • The discount rate determines the present value of future rewards.

  • When the discount rate approaches 1, the future rewards are taken into account more strongly.

  • The objective of the MDPs is to calculate the optimal policy \(\pi^*\).

    • The policy that will maximize the value function \(V^\pi(s_0)\).

    • \(V^\pi(s_0)\) is the total expected reward if the agent follow \(\pi\) starting in \(s_0\):

\[V^\pi(s_0)= \mathbb{E}\left[G_0|s_0 \right] = \mathbb{E}\left[ \sum_{t=0}^{\infty}\gamma^t r(s_t,\pi(s_t))|s_0 \right]\]

  • So the optimal value function \(V^{\pi^*}\) is defined as:

\[\begin{split}\begin{aligned} V^{\pi^*}(s) &= \max_{\pi} V^\pi(s)\\ &= \max_{a}\mathbb{E}_{\pi^*}\left[G_t | s, a \right]\\ &= \max_{a}\mathbb{E}_{\pi^*}\left[R_{t+1} + \gamma G_{t+1} | s, a \right]\\ &= \max_{a}\mathbb{E}_{\pi^*}\left[R_{t+1} + \gamma V^{\pi^*}(s_{t+1}) | s, a \right]\\ &= \max_{a}r(s,a)+\gamma\sum_{s'}p(s'|s,a)V^{\pi^*}(s')\\ \end{aligned}\end{split}\]

Dynamic Programming

  • We define how a MDP can be solved, but we need to discuss possible algorithms to do it.

  • MDPs are usually solved dynamic programming algorithms.

  • We will assume a finite MDP (finite horizon).

The Idea

  • We want to use the value functions to search for a good policy.

  • We have seen that we can obtain the optimal policy once we found the optimal value function.

  • The idea is to calculate the optimal value function.

Value Iteration

  • Value Iteration is an exact method.

  • It works in three steps:

    1. Initialize random policy

    2. Policy Evaluation

    3. Policy improvement

Pseudocode

_images/policy_iteration.png

Example

  • A robot that needs to either go on the cell on the top left or bottom right cell.

  • At first the policy is initialized randomly.

  • After applying policy iteration we converge to the optimal policy.

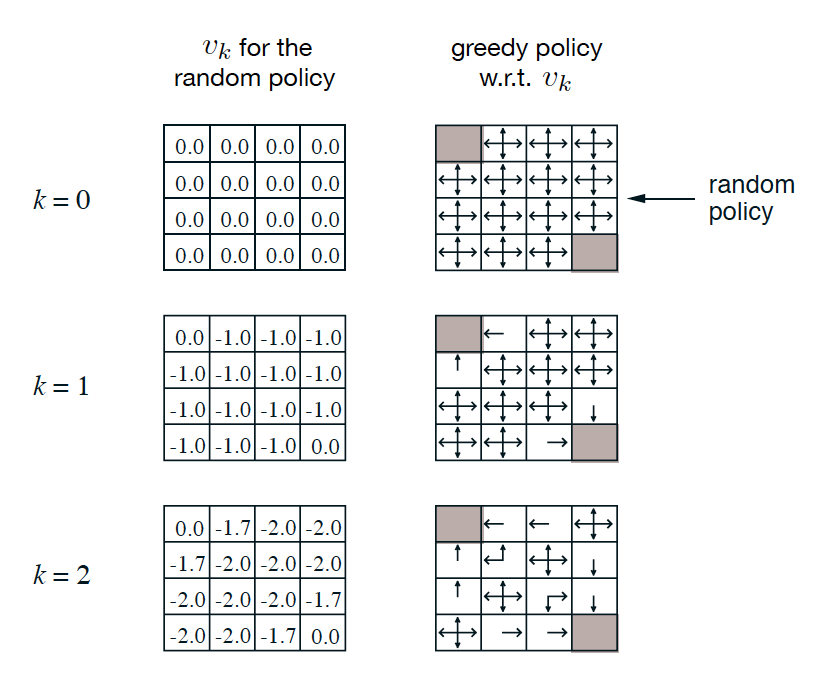
_images/value_iteration_01.png
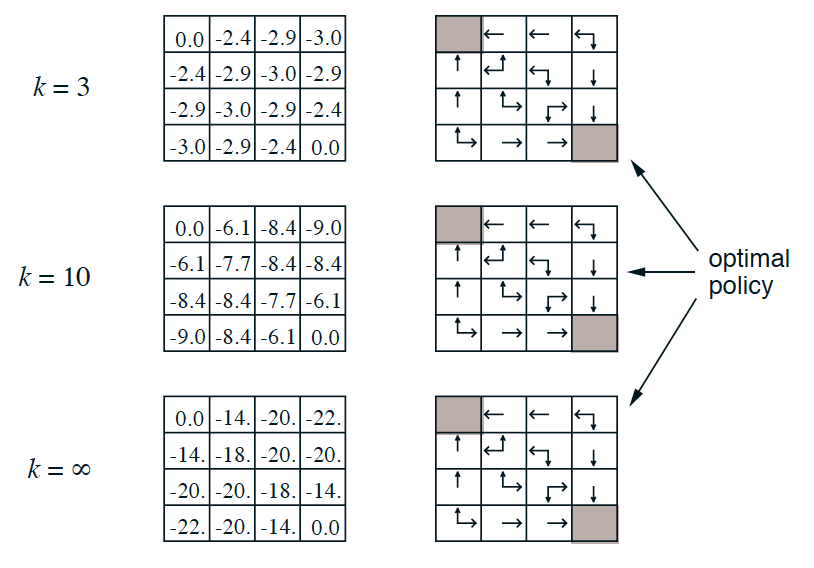
_images/value_iteration_02.png

Activity

  • Consider the following problems:

    • A Hallway consisting of 7 tiles.

    • The idea is for a robot to reach the centered tile.

    • It can start from any tile.

    • It can either move on the left or on the right.

    • Each time the robot moves it receive a reward of -1.

    • If it reaches the centered tile, it receives a reward of +10.

  • Model this as an MDP.

  • Solve it by hand.

  • Implement it in python.

Efficiency

  • Dynamic programming is very efficient for lots of problems.

  • It is also the case with Markov Decision Processes.